Презентация - Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс

РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ: «Аксиомы стереометрии. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ". ГЕОМЕТРИЯ 10 КЛАСС

Задание 1 Вставьте пропущенные слова Единственную плоскость можно задать через три точки, при этом они на одной прямой. 2) Если точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. 3) Две различные плоскости могут иметь только одну общую 4) Прямые являются в пространстве, если они не пересекаются и в одной плоскости. 5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке В α, то прямые а и b не лежат две прямую параллельными лежат скрещивающиеся

Задание 2 Определите: верно, ли утверждение? 1. Если прямая проходит через вершину треугольника, то она лежит в плоскости треугольника. 2. Если прямые не пересекаются, то они параллельны. 3. Прямая m параллельна прямой n , прямая m параллельна плоскости α. Прямая n параллельна плоскости α. 4. Все прямые пересекающие стороны треугольника лежат в одной плоскости. 5. Прямая АВ и точки С, D не лежат в одной плоскости. Могут ли прямые АВ и С D пересекаться? Нет Нет Да Да Нет

Задание 2 Определите: верно, ли утверждение? 6. Прямые АВ и С D пересекаются. Могут ли прямые АС и В D быть скрещивающимися? 7. Прямые а и в не лежат в одной плоскости. Можно ли провести прямую с , параллельную прямым а и в ? 8. Прямая а , параллельная прямой в, пересекает плоскость α. Прямая с параллельна прямой в. Может ли прямая с лежать в плоскости α? 9. Прямая а параллельна плоскости α. Существует ли на плоскости α прямые, непараллельные а? Нет Нет Нет Да

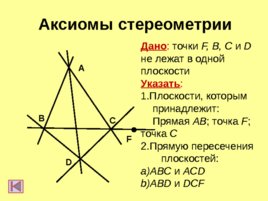
Аксиомы стереометрии C D B F A Дано : точки F, B, C и D не лежат в одной плоскости Указать : Плоскости, которым принадлежит: Прямая AB ; точка F ; точка С Прямую пересечения плоскостей: ABC и ACD ABD и DCF

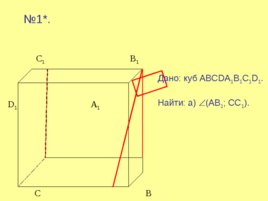
С 1 B 1 D 1 A 1 C B D A № 1 . Дано: куб ABCDA 1 B 1 C 1 D 1 . Найти: а) (АВ 1 ; СС 1 ).

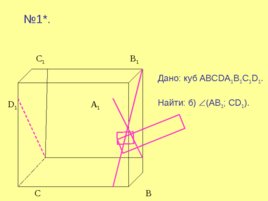
С 1 B 1 D 1 A 1 C B D A № 1 . Дано: куб ABCDA 1 B 1 C 1 D 1 . Найти: б) (АВ 1 ; С D 1 ).

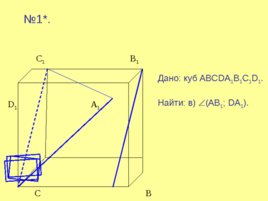
С 1 B 1 D 1 A 1 C B D A № 1 . Дано: куб ABCDA 1 B 1 C 1 D 1 . Найти: в) (АВ 1 ; DA 1 ).

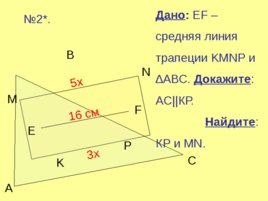
Дано : EF – средняя линия трапеции KMNP и ABC . Докажите : АС КР. Найдите : КР и MN . A B C K M N P E F 3x 5x 16 см № 2 .

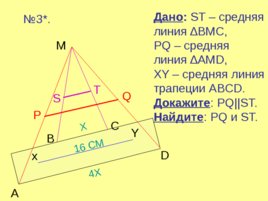
Дано : ST – средняя линия BMC, PQ – средняя линия AMD, XY – средняя линия трапеции ABCD. Докажите : PQ ST . Найдите : PQ и ST . № 3 . A B C D M 4 Х Х 16 СМ P Q S T x Y

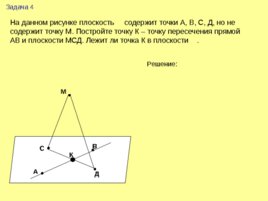
На данном рисунке плоскость содержит точки А, В, С, Д, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСД. Лежит ли точка К в плоскости . А В С Д М Задача 4 К Решение:

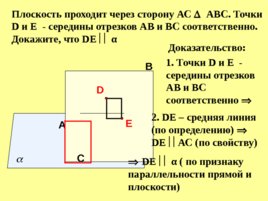
A В С Плоскость проходит через сторону АС АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE α D E Доказательство: 1. Точки D и E - середины отрезков АВ и BC соответственно 2. DE – средняя линия (по определению) DE АС (по свойству) DE α ( по признаку параллельности прямой и плоскости)

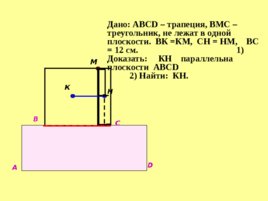
Дано: АВС D – трапеция, ВМС – треугольник, не лежат в одной плоскости. ВК КМ, СН НМ, ВС 12 см. 1) Доказать: КН параллельна плоскости АВС D 2) Найти: КН. А В С D М К Н

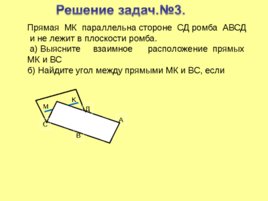
Прямая МК параллельна стороне СД ромба АВСД и не лежит в плоскости ромба. а) Выясните взаимное расположение прямых МК и ВС б) Найдите угол между прямыми МК и ВС, если M K А С Д В