Презентация - Нестандартные способы решения задач на ОГЭ
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 82%
- Слайдов: 45
- Просмотров: 5103
- Скачиваний: 2294
- Размер: 1.11 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Решение задач ОГЭ «Модуль геометрия» Часть 2
Решение задач ОГЭ «Модуль геометрия» Часть 2 Решение нестандартных задач
Решение нестандартных задач Урок математики 2 класс «Решение нестандартных геометрических задач»
Урок математики 2 класс «Решение нестандартных геометрических задач» Нестандартные способы решения квадратных уравнений
Нестандартные способы решения квадратных уравнений Элементы комбинаторики. Способы решения комбинаторных задач
Элементы комбинаторики. Способы решения комбинаторных задач Решение задач способом решения уравнения
Решение задач способом решения уравнения Упражнение №2. Для устного счёта по теме: "Функционально - графический способ решения задач с параметром"
Упражнение №2. Для устного счёта по теме: "Функционально - графический способ решения задач с параметром"
Слайды и текст этой онлайн презентации
Слайд 1

Нестандартные способы решения задач на ОГЭ
Подготовила: Князева Ольга Юрьевна учитель математики МОУСОШ№5 с.Журавского 2017 г.
Подготовила: Князева Ольга Юрьевна учитель математики МОУСОШ№5 с.Журавского 2017 г.
Слайд 2

ГЕОМЕТРИЯ
Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение. (В. Произволов)
Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение. (В. Произволов)
Слайд 3

Вычисление площадей фигур на клетчатой бумаге
Слайд 4

«Не бойтесь формул! Учитесь владеть этим инструментом человеческого гения! В формулах заключено величие и могущество разума…» Марков А. А.
Слайд 5
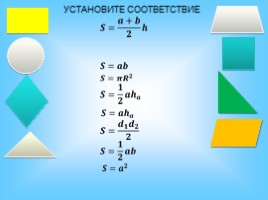
УСТАНОВИТЕ СООТВЕТСТВИЕ
Слайд 6
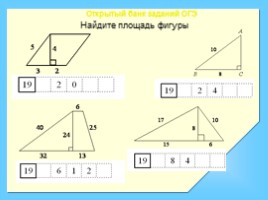
Найдите площадь фигуры
Открытый банк заданий ОГЭ
Открытый банк заданий ОГЭ
Слайд 7
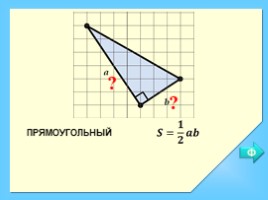
ПРЯМОУГОЛЬНЫЙ
?
?
Ф
?
?
Ф
Слайд 8
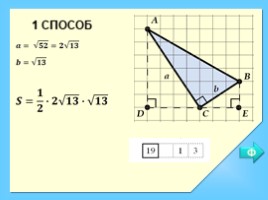
1 СПОСОБ
Ф
Ф
Слайд 9
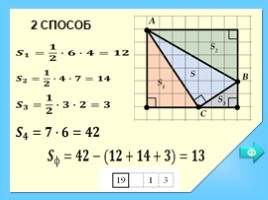
2 СПОСОБ
Ф
Ф
Слайд 10

Георг Пик
Георг Александр Пик, австрийский математик (10.08.1859 — 13.07.1942)
Георг Александр Пик, австрийский математик (10.08.1859 — 13.07.1942)
Слайд 11

Формула была открыта в 1899 г.
Г – количество узлов на границе треугольника (на сторонах и вершинах): В – количество узлов внутри треугольника; * Под «узлами» имеется ввиду пересечение линий.
Площадь искомой фигуры можно найти по формуле:
Г – количество узлов на границе треугольника (на сторонах и вершинах): В – количество узлов внутри треугольника; * Под «узлами» имеется ввиду пересечение линий.
Площадь искомой фигуры можно найти по формуле:
Слайд 12
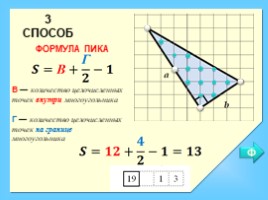
3 СПОСОБ
ФОРМУЛА ПИКА
В — количество целочисленных точек внутри многоугольника Г — количество целочисленных точек на границе многоугольника
Ф
ФОРМУЛА ПИКА
В — количество целочисленных точек внутри многоугольника Г — количество целочисленных точек на границе многоугольника
Ф
Слайд 13
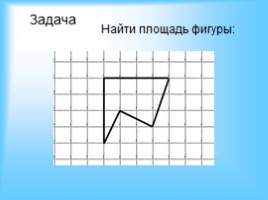
Задача
Найти площадь фигуры:
Найти площадь фигуры:
Слайд 14
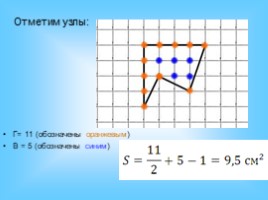
Г= 11 (обозначены оранжевым)
В = 5 (обозначены синим)
Отметим узлы:
Отметим узлы:
Слайд 15
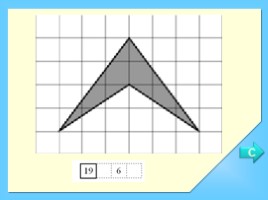
С
Слайд 16
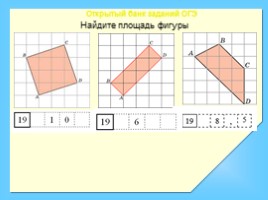
Найдите площадь фигуры
Открытый банк заданий ОГЭ
Открытый банк заданий ОГЭ
Слайд 17
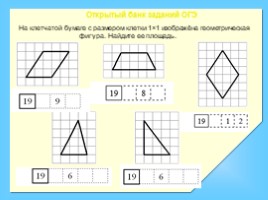
На клетчатой бумаге с размером клетки 1×1 изображёна геометрическая фигура. Найдите ее площадь.
Открытый банк заданий ОГЭ
Открытый банк заданий ОГЭ
Слайд 18
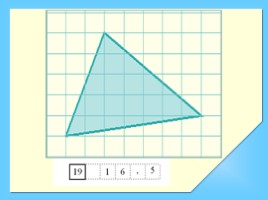
Слайд 19
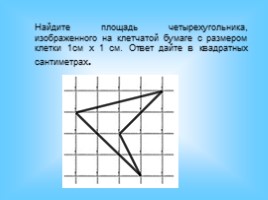
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1 см. Ответ дайте в квадратных сантиметрах.
Слайд 20

Алгебра
Решение задач на смеси и сплавы
Решение задач на смеси и сплавы
Слайд 21

Задачи на «концентрацию», на «смеси и сплавы»
-концентрация(доля чистого вещества в смеси) -количество чистого вещества в смеси -масса смеси. масса смеси х концентрация = количество чистого вещества.
-концентрация(доля чистого вещества в смеси) -количество чистого вещества в смеси -масса смеси. масса смеси х концентрация = количество чистого вещества.
Слайд 22

Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор соли, его масса равна 180 + 20 = 200 грамм.
Концентрация соли (процентное содержание соли) - это отношение количества соли к количеству раствора, записанное в процентах - (20 : 200) ·100 = 10%
Концентрация соли (процентное содержание соли) - это отношение количества соли к количеству раствора, записанное в процентах - (20 : 200) ·100 = 10%
Слайд 23
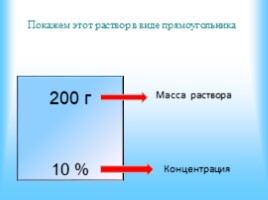
Покажем этот раствор в виде прямоугольника
200 г 10 %
Масса раствора
Концентрация
200 г 10 %
Масса раствора
Концентрация
Слайд 24

Возьмем 15 кг цемента и 45 кг песка, высыпим содержимое ведер в ящик и тщательно перемешаем цемент с песком. Получим смесь цемента с песком, её масса равна 15 кг + 45 кг = 60 кг.
Концентрация цемента (процентное содержание цемента) – это отношение количества цемента к количеству смеси, записанное в процентах – (15 : 60) ·100 = 25%
Концентрация цемента (процентное содержание цемента) – это отношение количества цемента к количеству смеси, записанное в процентах – (15 : 60) ·100 = 25%
Слайд 25
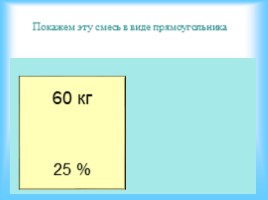
Покажем эту смесь в виде прямоугольника
60 кг 25 %
60 кг 25 %
Слайд 26

Задача №1
Имеется 30 кг 26% го раствора соли. Требуется получить 40% раствор соли. Сколько кг 50% раствора соли нужно добавить?
30 кг 26 %
50 %
40 %
Имеется
Нужно добавить
Требуется получить
=
+
х кг
(30+х )кг
Имеется 30 кг 26% го раствора соли. Требуется получить 40% раствор соли. Сколько кг 50% раствора соли нужно добавить?
30 кг 26 %
50 %
40 %
Имеется
Нужно добавить
Требуется получить
=
+
х кг
(30+х )кг
Слайд 27
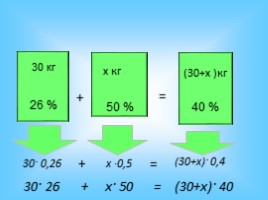
30 кг
26 %
50 %
40 %
=
+
х кг
(30+х )кг
30· 0,26
х ·0,5
(30+х)· 0,4
=
+
30· 26 + х· 50 = (30+х)· 40
50 %
40 %
=
+
х кг
(30+х )кг
30· 0,26
х ·0,5
(30+х)· 0,4
=
+
30· 26 + х· 50 = (30+х)· 40
Слайд 28

Задача №2
Из чаши, содержащей 300 граммов 6% раствора уксусной кислоты, отлили некоторое количество этого раствора и добавили такое же количество воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты
Из чаши, содержащей 300 граммов 6% раствора уксусной кислоты, отлили некоторое количество этого раствора и добавили такое же количество воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты
Слайд 29
Нарисуйте и заполните рисунок
Было
Отлили
Добавили
Получили
Было
Отлили
Добавили
Получили
Слайд 30

Проверим!
300 г 6%
Было
Отлили
Добавили
Получили
х г 6%
х г 0%
300 г 2%
-
=
+
300 · 6 – 6х + х·0 = 300 · 2
Ответ: 200 г.
300 г 6%
Было
Отлили
Добавили
Получили
х г 6%
х г 0%
300 г 2%
-
=
+
300 · 6 – 6х + х·0 = 300 · 2
Ответ: 200 г.
Слайд 31

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Решение:
Х 30%
У 60%
10 0%
Х+у+10 36%
Х+у+10 41%
10 50%
У 60%
Х 30%
Составим систему уравнений:
30х+60у+10*0=(х+у+10)*36, 30х+60у+10*50=(х+у+10)*41. Решая ее, получаем х=60, у=30. Ответ: 60.
Решение:
Х 30%
У 60%
10 0%
Х+у+10 36%
Х+у+10 41%
10 50%
У 60%
Х 30%
Составим систему уравнений:
30х+60у+10*0=(х+у+10)*36, 30х+60у+10*50=(х+у+10)*41. Решая ее, получаем х=60, у=30. Ответ: 60.
Слайд 32

Метод Пирсона
при решении задач на смеси и сплавы
Слайд 33

Теоретические основы
решения задач «на смеси, сплавы»
Примем некоторые допущения:
Все получающиеся сплавы или смеси однородны.
При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
Определение. Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах.
Терминология:
процентное содержание вещества;
концентрация вещества;
массовая доля вещества. Всё это синонимы.
Слайд 34

Готовим раствор определенной концентрации. Имеется 2 раствора с более высокой и менее высокой концентрацией, чем нужно.
Обозначим массу 1-го раствора m 1, а 2-го m 2, тогда при смешивании масса смеси будет равна сумме этих масс. Массовая доля растворённого вещества в 1-м растворе – q 1, во 2-м – q 2, а в их смеси – q 3. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах: m 1 q 1 + m 2q2 =q3(m 1 + m 2), m 1(q 1 – q 3) = m 2(q 3 – q2)
Отношение массы 1-го раствора к массе 2-го раствора это отношение разности массовых долей растворённого вещ-ва в смеси и в 2-м растворе к разности величин в 1-м растворе и в смеси.
Слайд 35

При решении задач на растворы с разными концентрациями чаще всего применяют квадрат Пирсона.
При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
q1 q3 — q2 q3 q2 q1 — q3
q1 q3 — q2 q3 q2 q1 — q3
Слайд 36

Задача 3. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%?
Решение:
Слайд 37

Задача 4. Из сосуда, доверху наполненного 97% раствором кислоты, отлили 2 литра жидкости и долили 2 литра 45% раствора этой же кислоты. После этого в сосуде получился 81% раствор кислоты. Сколько литров раствора вмещает сосуд?
Решение:
97%
81%
45%
Слайд 38

Задача 5 .
Смешали 500 г 10%-го раствора соли и 400 г 55%-го раствора соли. Определите концентрацию соли в смеси.
Решение:
Слайд 39

Задача 6. Имеются два слитка, содержащие медь. Масса второго слитка на 3 кг больше, чем масса первого слитка. Процентное содержание меди в первом слитке – 10%, во втором – 40%. После сплавления этих двух слитков, получился слиток, процентное содержание меди в котором 30%. Определить массу полученного слитка.
Решение:
Слайд 40

Задача 7. Сплавили 300 г сплава олова и меди, содержащего 60% олова, и 900г сплава олова и меди, содержащего 80% олова. Сколько процентов олова в получившемся сплаве?
Решение:
Слайд 41
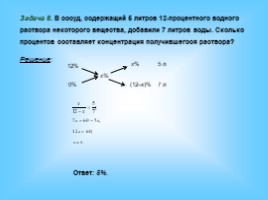
Задача 8. В сосуд, содержащий 5 литров 12-процентного водного
раствора некоторого вещества, добавили 7 литров воды. Сколько
процентов составляет концентрация получившегося раствора?
Решение:
Ответ: 5%.
Ответ: 5%.
Слайд 42

Реши сам!
1) Смешали 3 литра 25-процентного водного раствора некоторого вещества с 12 литрами 15-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? 2) Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго? 3) Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. 4) Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
1) Смешали 3 литра 25-процентного водного раствора некоторого вещества с 12 литрами 15-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? 2) Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго? 3) Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. 4) Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
Слайд 43

Математика-наука интересная, сложная,
поэтому нельзя упускать ни одной возможности
сделать её более доступной!
Слайд 44

Спасибо за внимание
Слайд 45

Если вы хотите научиться плавать,
то смело входите в воду, а если хотите научиться решать задачи,
то решайте их!
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
