Презентация - Упражнение №2. Для устного счёта по теме: "Функционально - графический способ решения задач с параметром"

УПРАЖНЕНИЕ №2
для устного счёта по теме:
"ФУНКЦИОНАЛЬНО - ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРОМ"
,

СПРАВОЧНЫЙ МАТЕРИАЛ
Функционально-графический способ решения задач с параметром
Задачу с параметром можно рассматривать как функцию f (x; a) = 0.
1. Строим графический образ.
Схема решения
2. Пересекаем полученный график прямыми параллельными оси абсцисс.
3. «Считываем» нужную информацию.

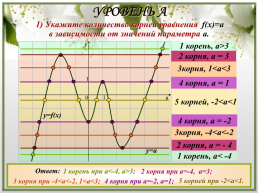
УРОВЕНЬ A
1) Укажите количество корней уравнения f(x)=a в зависимости от значений параметра а.
1 корень, а>3
2 корня, а = 3
3корня, 14 корня, а = 1
5 корней, -2y=f(x)
4 корня, а = -2
3корня, -42 корня, а = - 4
y=a
1 корень, а< -4
1 корень при а<-4, а>3;
2 корня при а=-4, а=3;
5 корней при -2<а<1.
3 корня при -4<а<-2, 1<а<3;
4 корня при а=-2, а=1;

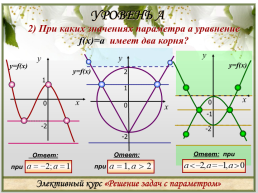
УРОВЕНЬ A
2) При каких значениях параметра а уравнение f(x)=a имеет два корня?
y=f(x)

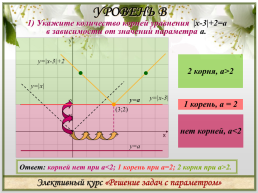
УРОВЕНЬ В
1) Укажите количество корней уравнения |x-3|+2=a в зависимости от значений параметра а.
2 корня, а>2
y=|x-3|+2
y=|x|
y=|x-3|
1 корень, а = 2
(3;2)
нет корней, а<2
Ответ: корней нет при а<2; 1 корень при а=2; 2 корня при а>2.

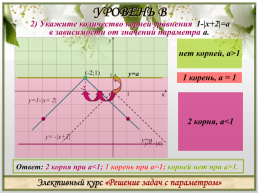
УРОВЕНЬ В
2) Укажите количество корней уравнения 1-|x+2|=a в зависимости от значений параметра а.
нет корней, а>1
(-2;1)
1 корень, а = 1
2 корня, а<1
у=1-|x+ 2|
y= -|x+2|
y= -|x|
Ответ: 2 корня при а<1; 1 корень при а=1; корней нет при а>1.

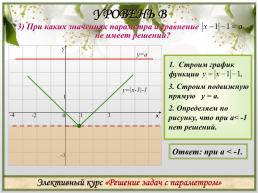
УРОВЕНЬ В
3. Строим подвижную прямую у = а.
y=|x-1|-1
2. Определяем по рисунку, что при а< -1 нет решений.
Ответ: при а < -1.

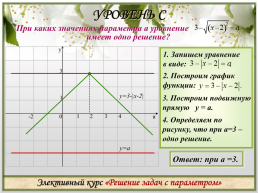
УРОВЕНЬ С
y=3-|x-2|
3. Построим подвижную прямую у = а.
4. Определяем по рисунку, что при а=3 – одно решение.
Ответ: при а =3.