Презентация - Графические приемы решения задач с параметром

Графические приемы решения задач с параметром

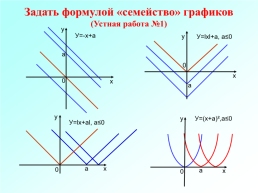
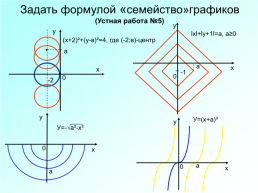
Задать формулой «семейство» графиков (Устная работа №1)
у
У=-х+а
у
У=lхl+а, а≤0
а
х
х
а
у
у
У=(х+а)²,а≤0
У=lх+аl, а≤0
а
х
а
х

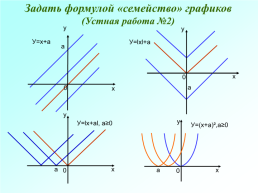
Задать формулой «семейство» графиков (Устная работа №2)
у
у
У=х+а
У=lхl+а
а
х
а
х
у
у
У=lх+аl, а≥0
У=(х+а)²,а≥0
а
х
а
х

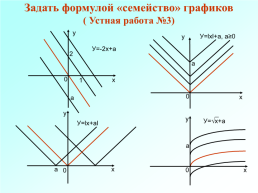
Задать формулой «семейство» графиков ( Устная работа №3)
у
У=lхl+а, а≥0
у
У=-2х+а
а
х
х
а
у
у
У=√х+а
У=lх+аl
а
а
х
х

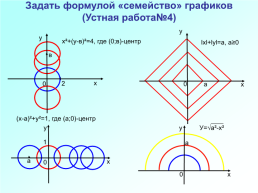
Задать формулой «семейство» графиков (Устная работа№4)
у
у
х²+(у-в)²=4, где (0;в)-центр
lхl+lуl=а, а≥0
в
х
а
х
(х-а)²+у²=1, где (а;0)-центр
у
У=√а²-х²
у
а
а
х
х

Задать формулой «семейство»графиков (Устная работа №5)
у
у
lхl+lу+1l=а, а≥0
(х+2)²+(у-в)²=4, где (-2;в)-центр
а
а
х
х
-1
-2
у
У=(х+а)³
у
У=-√а²-х²
х
а
х
а

№3
При каких значениях параметра а система уравнений имеет 4 решения? 8 решений? Не имеет решений?
lхl+lуl=3 х²+у²=а
у
√а
R=√а
В
ΔАВС-прямоугольный, равнобедренный; Проведем ОК┴АВ,
1,5√2
ОВ=3, АВ=3√2 ОК=КВ=АК=1,5√2;
К
а≥0 1,5√2-3
Ответ: 1) 4 решения при а=4,5 и а=9; 2) Система уравнений Имеет 8 решений при 4,59.
А
х
-3

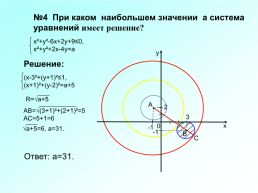
№4 При каком наибольшем значении а система уравнений имеет решение?
х²+у²-6х+2у+9≤0, х²+у²+2х-4у=а
у
Решение:
(х-3²+(у+1)²≤1, (х+1)²+(у-2)²=а+5
R=√а+5
А
АВ=√(3+1)²+(2+1)²=5 АС=5+1=6
х
-1
√а+5=6, а=31.
-1
В
С
Ответ: а=31.

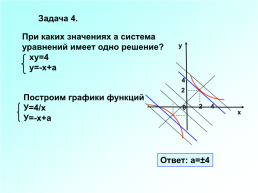
Задача 4.
При каких значениях а система уравнений имеет одно решение? ху=4 у=-х+а
у
Построим графики функций У=4/х У=-х+а
х
Ответ: а=±4

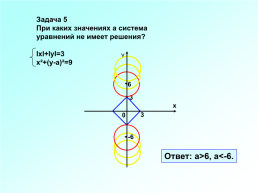
Задача 5 При каких значениях а система уравнений не имеет решения? lхl+lуl=3 х²+(у-а)²=9
у
х
-6
Ответ: а>6, а<-6.

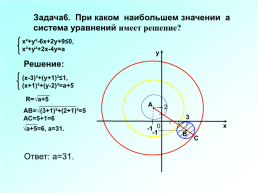
Задача6. При каком наибольшем значении а система уравнений имеет решение?
х²+у²-6х+2у+9≤0, х²+у²+2х-4у=а
у
Решение:
(х-3)²+(у+1)²≤1, (х+1)²+(у-2)²=а+5
R=√а+5
А
АВ=√(3+1)²+(2+1)²=5 АС=5+1=6
х
-1
√а+5=6, а=31.
-1
В
С
Ответ: а=31.

Презентация к уроку
Графические приемы решения задач с параметром

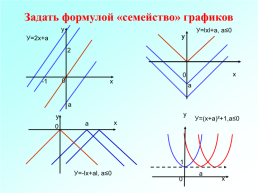
Задать формулой «семейство» графиков
у
У=lхl+а, а≤0
у
у
У=2х+а
х
-1
х
а
а
у
у
У=(х+а)²+1,а≤0
х
а
У=-lх+аl, а≤0
а
х

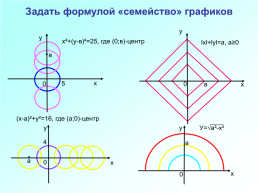
Задать формулой «семейство» графиков
у
у
х²+(у-в)²=25, где (0;в)-центр
lхl+lуl=а, а≥0
в
х
а
х
(х-а)²+у²=16, где (а;0)-центр
у
У=√а²-х²
у
а
а
х
х

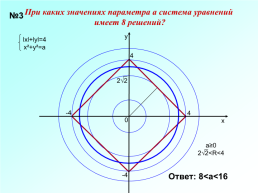
При каких значениях параметра а система уравнений имеет 8 решений?
№3
у
lхl+lуl=4 х²+у²=а
2√2
-4
х
а≥0 2√2-4
Ответ: 8<а<16

№4
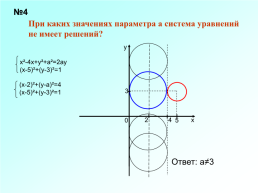
При каких значениях параметра а система уравнений не имеет решений?
у
х²-4х+у²+а²=2ау (х-5)²+(у-3)²=1
(х-2)²+(у-а)²=4 (х-5)²+(у-3)²=1
х
Ответ: а≠3

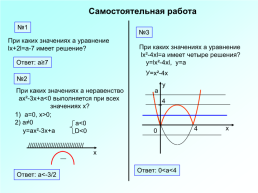
Самостоятельная работа
№1
№3
При каких значениях а уравнение lх+2l=а-7 имеет решение?
При каких значениях а уравнение lх²-4хl=а имеет четыре решения?
Ответ: а≥7
у=lх²-4хl, у=а
У=х²-4х
№2
у
При каких значениях а неравенство ах²-3х+а<0 выполняется при всех значениях х?
а
а=0, х>0; 2) а≠0
а<0 D<0
х
у=ах²-3х+а
///////////////////////////////
х
Ответ: 0<а<4
Ответ: а<-3/2

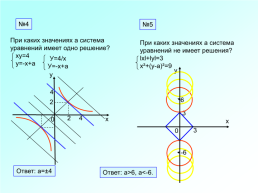
№4
№5
При каких значениях а система уравнений имеет одно решение? ху=4 у=-х+а
При каких значениях а система уравнений не имеет решения? lхl+lуl=3 х²+(у-а)²=9
У=4/х У=-х+а
у
у
х
х
-6
Ответ: а=±4
Ответ: а>6, а<-6.