Презентация - Задания типа 18

Задания типа 18

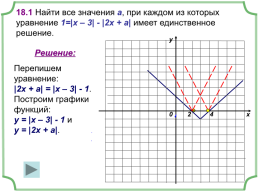
18.1 Найти все значения а, при каждом из которых уравнение 1=|x – 3| - |2x + a| имеет единственное решение.
Решение: Перепишем уравнение: |2x + a| = |x – 3| - 1. Построим графики функций: у = |x – 3| - 1 и у = |2x + a|.

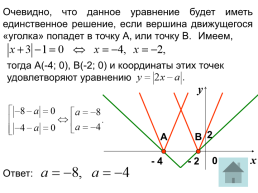
Очевидно, что данное уравнение будет иметь единственное решение, если вершина движущегося «уголка» попадет в точку с координатами (2; 0) или (4; 0). Следовательно, координаты этих точек удовлетворяют уравнению у = |2x + a|. Значит, 0 = |4 + a| или 0 = |8 + a| а = - 4 а = - 8. Ответ: - 8 или – 4.

ПАМЯТКА
x, если х ≥ 0
|x| =
Пользоваться определением модуля
– x, если х ˂ 0
|x|< а →
-а < x < а
|x|> а →
x < -а и х > а
А так же
Знать и строить: уравнение, линию, алгоритм построения:
y = kx + b – линейная,
прямая
надо иметь, хотя бы, 2 точки
y = аx² + bх + с – квадратная,
парабола
*направление ветвей
*пересечение с ОХ
*х₀ = -b/2a – абсцисса вершины – ось симметрии
*выделять полный квадрат
x² + y² = R² – окружность,
Центр (0;0), R - радиус
(x-а)² + (y-b)² = R² – окружность,
Центр (a; b), R - радиус
k > 0
y = - гипербола
линии выше ОХ
оставляем
y = |f(x)|
точки оси ОХ
y = f(x)
линии ниже ОХ
симметрично
график
график
в верхнюю полуплоскость

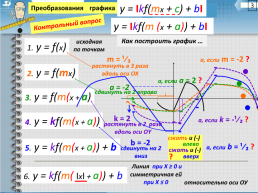
y = Ikf(mx + c) + bI
Преобразования
графика
y = Ikf(m (x + a)) + bI
Контрольный вопрос
Как построить график …
исходная по точкам
1. y = f(х)
m = ¹∕₃
а, если m = -2 ?
-
растянуть в 3 раза вдоль оси ОХ
2. y = f(mх)
-
❹
а, если a = 2 ?
-
-
❸
a = -2
сдвинуть на 2 вправо
3. y = f(m(х + a)
-
-
-
-
❷
-
-
-
-
-
-
-
-
-
❺
-
k = 2
4. y = kf(m(х + a))
-
а, если k = -¹∕₂ ?
-
растянуть в 2 раза вдоль оси ОY
-
сжать и (-)
b = -2
5. y = kf(m(х + a)) + b
влево
а, если b = ¹∕₂ ?
сдвинуть на 2 вниз
сжать и (-)
?
вверх
Линия при Х ≥ 0 и
6. y = kf(m( IхI + a)) + b
симметричная ей при Х ≤ 0
относительно оси ОУ

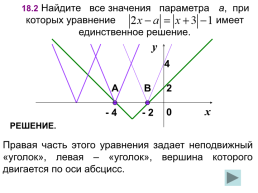
18.2 Найдите все значения параметра а, при которых уравнение имеет единственное решение.
А
В
РЕШЕНИЕ.
Правая часть этого уравнения задает неподвижный «уголок», левая – «уголок», вершина которого двигается по оси абсцисс.

у
х
- 4
- 2

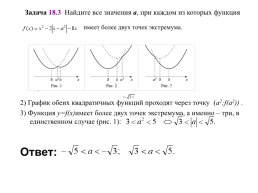
Задача 18.3 Найдите все значения a, при каждом из которых функция имеет более двух точек экстремума.
Решение. 1. Функция f имеет вид:
а) при
, поэтому ее график есть часть параболы
с ветвями, направленными вверх, и осью симметрии x=5;
б) при
, поэтому ее график есть часть параболы с
ветвями, направленными вверх, и осью симметрии x=3.
Все возможные виды графика функции f(x) показаны на рисунках:

Задача 18.3 Найдите все значения a, при каждом из которых функция
имеет более двух точек экстремума.
2) График обеих квадратичных функций проходят через точку (a2;f(a2)) . 3) Функция y=f(x)имеет более двух точек экстремума, а именно – три, в единственном случае (рис. 1): Ответ:

18.4 Найдите все положительные значения a, при каждом из которых система уравнений имеет единственное решение.
x – 9, если х ≥ 0 ,
По определению модуля:
|x| – 9 =
– x – 9, если х ˂ 0 ,
( –1)²
х²
х² =
( – х)²
∙ х² =
= ( –1∙ х)² =
Заметим:
=( –1)²
(-(х+9))²
∙(х+9)²
= (х+9)²
(– x – 9)²=
(- х – 9)² + (у – 5)² = 9
(х – 9)² + (у – 5)² = 9
(х + 9)² + (у – 5)² = 9
х ≥ 0
х < 0
График уравнения - совокупность двух окружностей.
R = 3
центры
(9; 5)
(-9; 5)

8
Первые уравнения
Второе уравнение
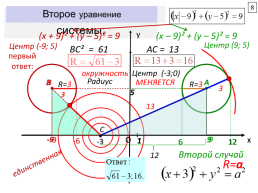
График 1-го уравнения системы:
у
у
(х + 9)² + (у – 5)² = 9
(х – 9)² + (у – 5)² = 9
Центр (9; 5)
Центр (-9; 5)
BC²
= 61
АС =
первый ответ:
окружность
Центр (-3;0)
Радиус
МЕНЯЕТСЯ
В
B
А
А
R=3
R=3
●
●
С
●
-9
-9
О
О
х
х
-6
-3
Второй случай
R=а
единственная

10
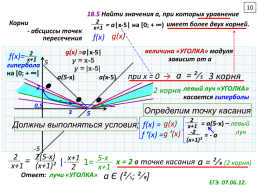
18.5 Найти значения а, при которых уравнение
Корни
имеет более двух корней.
= a|x-5|
на [0; + ∞)
- абсциссы точек
g(x)
f(x)
пересечения
величина «УГОЛКА» модуля
g(x) =a|x-5|
f(x)=
зависит от а
y = x-5
гипербола
y = |x-5|
на [0; + ∞]
а
= ²⁄5
3 корня
при х = 0
→
a(5-x)
a(x-5)
❶
левый луч «УГОЛКА» касается гиперболы
2 корня
●
❷
❸
●
●
●
1 корень
2 корня
0,5
●
Определим точку касания
g(x)
= a(5-x) – левый луч
Должны выполняться условия:
f(x) =
g ′(x)
f ′(x) =
= - a
-5
=
|∙
1=
а
= ²⁄9 (2 корня)
х = 2 в точке касания
а Є
(²⁄5; ²⁄9]
Ответ:
лучи «УГОЛКА»
ЕГЭ. 07.06.12.

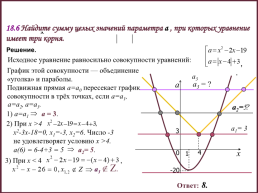
Решение.
Исходное уравнение равносильно совокупности уравнений:
График этой совокупности — объединение «уголка» и параболы.
а3 = ?
Подвижная прямая а=а0 пересекает график совокупности в трёх точках, если а=а1,
а=а2,
а=а3.
а2= ?
а2=5
а1= 3
Ответ: 8.

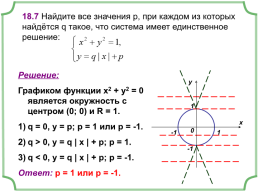
18.7 Найдите все значения р, при каждом из которых найдётся q такое, что система имеет единственное решение:
Решение: Графиком функции х2 + у2 = 0 является окружность с центром (0; 0) и R = 1. q = 0, у = р; р = 1 или р = -1. q > 0, y = q | x | + p; p = 1. q < 0, y = q | x | + p; p = -1. Ответ: р = 1 или р = -1.

18.8
Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно 4 решения.
Решение. Преобразуем данную систему:
Пусть t = y – 3, тогда система примет вид:
Заметим, что количество решений полученной системы совпадает с количеством решений исходной системы. Построим графики уравнений (1) и (2) в системе координат Oxt.

18.8
График первого уравнения – ромб, диагонали которого, равные 8 и 6, лежат на осях Ох и Оt, а графиком второго уравнения является окружность с центром в начале координат и радиусом r = a. Графики уравнений системы имеют ровно четыре общих точки, и, следовательно, система имеет ровно 4 решения, тогда и только тогда, когда окружность либо вписана в ромб, либо ее радиус удовлетворяет условию 3 < r < 4.
В первом случае радиус окружности является высотой прямоугольного треугольника с катетами 3 и 4, откуда
В втором случае получаем 3 <a < 4, откуда −4 < a < −3; 3 < a < 4.
Ответ: а =  2,4; −4 < a < −3; 3 < a < 4.