Презентация - Комбинаторика и ее применение к подсчету вероятностей

Комбинаторика и ее применение к подсчету вероятностей
Дисциплины: ЕН.01 Математика, ЕН.01 Элементы высшей математики, 2 курс Разработчик: Латышева Н.Л.
Государственное бюджетное профессиональное образовательное учреждение Воронежской области «Воронежский государственный промышленно-гуманитарный колледж»

Содержание

Историческая справка Некоторые элементы комбинаторики были известны в Индии еще во 2 веке до н.э. Индийцы умели вычислять сочетания. В 12 веке Бхаскара (1114-1185) вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали сочетания в связи с применением их в поэтике – науке о структуре стиха. 2200 лет назад Архимед написал трактат «Стомахион», содержание и смысл названия которого в течение столетий были покрыты мраком. И лишь недавно историки математики обнаружили, что он содержит решение довольно сложной комбинаторной задачи. Проблема, изложенная в трактате, оказалась столь непростой, что на ее решение современными средствами потребовалось 6 недель. Комбинаторика как наука стала развиваться в 17 веке параллельно с возникновением теории вероятностей. Пищу для комбинаторных размышлений математиков давали также азартные игры и потребности секретных служб государств в развитии криптографии.

Историческая справка Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье, Г. Галилею и французским ученым Б. Паскалю и П. Ферма. В 17 в. П. Эригон и Н. Тарталья независимо друг от друга получают формулу числа сочетаний. В 1656 г. в книге «Теория и практика арифметики» А. Такке посвящает сочетаниям и перестановкам целую главу. Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1665 г. работы «Рассуждение о комбинаторном искусстве», в которой впервые дано научное обоснование теории сочетаний и перестановок. Лейбниц вводит специальные символы и термины, выводит свойства и строит таблицы сочетаний, рассуждает о приложениях комбинаторики, предрекает ей блестящее будущее и широкое применение. В 1713 г. Я. Бернулли изучает размещения. Современная символика была предложена разными авторами в 19 в. Значительный вклад в развитие комбинаторики внес Л. Эйлер.

Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов заданного множества.  Два основных правила комбинаторики: Правило умножения (правило «и»). Согласно ему, если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару A и B можно выбрать n·m способами.  Это правило обобщается на произвольную длину последовательности. Правило сложения (правило «или»). Оно утверждает, что, если элемент A можно выбрать n способами, а элемент B можно выбрать m способами, то выбрать A или B можно n + m способами. Виды комбинаций Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке. Размещениями из n элементов по m называются такие выборки, которые, имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения. Неупорядоченные выборки называются сочетаниями из n элементов по m. 

Формула числа перестановок
Пусть имеется n различных объектов.  Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно Символ n! называется факториалом и обозначает произведение всех целых чисел от 1до n.  По определению, считают, что  Пример всех перестановок из n=3 объектов (различных фигур) - на картинке справа. Согласно формуле, их должно быть ровно 6.

Формула числа размещений
Пусть имеется n различных объектов.  Будем выбирать из них m объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по m, а их число равно Пример всех размещений из n=3n=3 объектов (различных фигур) по m=2m=2 - на картинке справа. Согласно формуле, их должно быть ровно 6. Число размещений с повторениями из n элементов по m определяется по формуле 

Формула числа сочетаний
Пусть имеется n различных объектов. Чтобы найти число сочетаний из n объектов по m, будем выбирать комбинации из m объектов все возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок. На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6). Общая формула, которая позволяет найти число сочетаний из n объектов по m имеет вид: Число сочетаний с повторениями из n элементов по m определяется по формуле  Взаимосвязь между формулами:

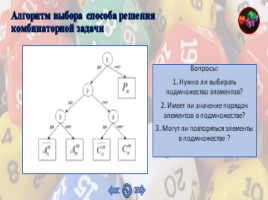
Алгоритм выбора способа решения комбинаторной задачи

Практикум Задача 1. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом? Задача 2. Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии 30-ти книг? Задача 3. Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 30-ти книг? Задача 4. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены различные премии? Задача 5. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены одинаковые призы?
решение
решение
решение
решение
решение

Применение комбинаторики в теории вероятностей. Задача 6. На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он не поставил 1-й и 2-й тома рядом? Задача 7. На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинакового формата расположены в произвольном порядке. Читатель, не глядя, берет 3 книги. Какова вероятность того, что он взял первые три тома? Задача 8. На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинаково оформлены и расположены в произвольном порядке. Читатель берет наугад 3 книги. Какова вероятность того, что он взял первые три тома? Задача 9. Из аквариума, в котором 6 сазанов и 4 карпа, сачком выловили 5 рыб. Какова вероятность того, что среди них окажется 2 сазана и 3 карпа?
решение
решение
решение
решение

Решение задачи 1
Определим общее число перестановок из 30 элементов по формуле P30=30! Чтобы вычислить число "лишних" перестановок, сначала определим, сколько вариантов, в которых 2-й том находится рядом с 1-ым справа от него. В таких перестановках 1-ый том может занимать места с первого по 29-е, а 2-й со второго по 30-е - всего 29 мест для этой пары книг. И при каждом таком положении первых двух томов остальные 28 книг могут занимать остальные 28 мест в произвольном порядке. Вариантов перестановки 28 книг P28=28! Всего "лишних" вариантов при расположении 2-го тома справа от 1-го получится 29·28! = 29!.  Аналогично рассмотрим случай, когда 2-й том расположен рядом с 1-ым, но слева от него. Получается такое же число вариантов 29·28! = 29!. Значит всего "лишних" перестановок 2·29!, а нужных способов расстановки 30!−2·29! Вычислим это значение. 30! = 29!·30; 30!−2·29! = 29!·(30−2) = 29!·28.  Итак, нам нужно перемножить все натуральные числа от 1 до 29 и еще раз умножить на 28.  Ответ: 2,4757335·1032.
В практикум

Решение задачи 2
Определим общее число размещений из 30 элементов по 15 по формуле  A3015 = 30·29·28·...·(30−15+1) = 30·29·28·...·16 = 202843204931727360000. Ответ: 202843204931727360000.
В практикум

Решение задачи 3
Мы решаем эту задачу в контексте работы дизайнера интерьеров, поэтому порядок следования на полке 15-ти выбранных внешне одинаковых книг не имеет значения. Нужно определить общее число сочетаний из 30 элементов по 15 по формуле  С3015 = 30!/(30 − 15)!/15! = 155117520. Ответ: 155117520.
В практикум

Решение задачи 4
Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом, так и порядком. Поскольку каждый фильм может получить призы как по одной, так и по нескольким номинациям, одни и те же фильмы могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 10 элементов по 5: 105 = 100 000 Ответ: 100 000.
В практикум

Решение задачи 5
Если по каждой номинации установлены одинаковые призы, то порядок фильмов в комбинации 5 призов значения не имеет, и число вариантов представляет собой число сочетаний с повторениями из 10 элементов по 5: Ответ: 2002.
В практикум

Решение задачи 6
Сначала определим вероятность события А, состоящего в том, что ребенок поставил 1-й и 2-й тома рядом.  Элементарное событие - некая расстановка книг на полке. Понятно, что общее число всех элементарных событий будет равно общему числу всех возможных перестановок P30=30!.  Число элементарных событий, благоприятствующих событию А, равно числу перестановок, в которых 1-й и 2-й тома стоят рядом. Мы рассматривали такие перестановки, решая предыдущую задачу, и получили 2·29! перестановок. Вероятность определяем делением числа благоприятствующих элементарных событий на число всех возможных элементарных событий:  P(A) = 2·29!/30! = 2·29!/(29!·30) = 2/30 = 1/15.  Событие В - ребенок не поставил 1-й и 2-й тома рядом - противоположно событию A, значит его вероятность P(B) = 1 − P(A) = 1−1/15 = 14/15 = 0,9333 Ответ: 0,9333.
В практикум

Решение задачи 7
Событие A - у читателя первые три тома. С учетом порядка выбора он мог взять их 6-ю способами. (Это перестановки из 3-ёх элементов P3 = 3! = 1·2·3 = 6, которые легко перечислить 123, 132, 213, 231, 312, 321.)  Таким образом, число благоприятствующих элементарных событий равняется 6.  Общее число возможных элементарных событий равно числу размещений из 6-ти по 3, т.е. A63 = 6·...·(6−3+1) = 6·5·4 = 120. P(A) = 6/120 = 1/20 = 0,05.  Ответ: 0,05.
В практикум

Решение задачи 8
Событие A - у читателя первые три тома. Это 1-й, 2-й и 3-й тома. Без учета порядка, в котором он выбирал книги, а только по конечному результату, он мог взять их одним способом. Число благоприятствующих элементарных событий - 1. Общее число возможных элементарных событий равно числу групп из 6-ти по 3, образованных без учета порядка следования элементов в группе, т.е. равно числу сочетаний С63 = 6!/3!/(6 - 3)! = 4·5·6/(1·2·3) = 4·5 = 20. P(A) = 1/20 = 0,05.  Ответ: 0,05.
В практикум

Решение задачи 9
Элементарное событие - "в сачке группа из 5 рыб". Событие A - "среди 5 пойманных рыб оказалось 3 карпа  и 2 сазана".  Пусть n - общее число всех возможных элементарных событий, оно равно числу способов сгруппировать по 5 рыб. Всего рыб в аквариуме 6 + 4 = 10. В процессе ловли сачком рыбы внешне неразличимы. Таким образом, "выловить 5 рыб из 10" означает сделать выборку типа сочетания из 10 по 5.  n = С105 = 10!/5!/(10 - 5)!  Вытащив сачок и заглянув в него, мы можем определить благоприятствующий это исход или нет, т.е. состоит ли улов из двух групп - 2 сазана и 3 карпа? Группа сазанов могла сформироваться выбором из 6 сазанов по 2. Причем всё равно, кто из них первым забрался в сачок, а кто вторым, т.о. это выборка типа сочетания из 6 по 2. Обозначим общее число таких выборок m1 . m1 = С62 = 6!/2!/(6 - 2)!  Аналогично общее число возможных групп по 3 карпа определяется числом сочетаний из 4 по 3. Обозначим его m2. m2 = С43 = 4!/3!/(4 - 3)!  Группы карпов и сазанов формируются в сачке независимо друг от друга, поэтому для подсчёта числа элементарных событий, благоприятствующих событию A, используем правило умножения ("и"-правило) комбинаторики. Итак, общее число благоприятствующих элементарных событий  m = m1·m2 = С62·С43  Вероятность события А определяем по формуле P(A) = m/n = С62·С43/С105 P(A) = 6!·4!·5!·(10 - 5)!/2!/(6 - 2)!/3!/(4 - 3)!/ 10! = 5/21 ≈ 0,238 Ответ: 0,238.

Проверь себя
Вопрос 1. В каком веке комбинаторика стала развиваться как наука? Ответ: в 17 веке Вопрос 2. Какой вид комбинаций применяется в задачах, где не важен процесс формирования выборки, а важен только результат? Ответ: сочетания Вопрос 3. Какое правило комбинаторики нужно применять, если необходимо найти вероятность совместного наступления двух событий? Ответ: правило умножения (и-правило) Вопрос 4. Что больше и во сколько раз: (n+1)!·n или n!·(n+1)? Ответ: первое число в n раз Вопрос 5. Приведите примеры областей знаний, в которых находит применение комбинаторика. Ответ: теория вероятностей, теория игр, криптография, поэтика и др.

Домашнее задание
Задача 1. Сколькими способами можно выбрать четырехзначное число, все цифры которого различны? Задача 2. Сколькими способами можно выбрать четырехзначное число, в десятичной записи которого нет нуля? Задача 3. Сколько четырехзначных чисел можно записать, используя без повторений все 10 цифр? Задача 4. Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек? Задача 5. В бригаде 4 женщины и 3 мужчин. Среди них разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?

Информационные источники: Андрухаев Х.Ь. Сборник задач по теории вероятностей: Учеб. Пособие / Х.М. Андрухаев; Под ред. А.С. Солодовникова. – 2-е изд., испр. И доп. – М.: Высш. Шк., 2005. – 174 с. Кессельман В.С. Удивительная история математики / В.С. Кессельман. – М. : ЭНАС-КНИГА, 2013. – 232 с. : ил. – (О чем умолчали учебники). Фадеева Л.Н., Жуков Ю.В., Лебедев А.В. Математика для экономистов: Теория вероятностей и математическая статистика. Задачи и упражнения. – Ь.: Эксмо, 2006. – 336 с. http://www.matburo.ru/tv_komb.php#form http://mathematichka.ru/school/combinatorics/combination.html