Презентация - Обратные тригонометрические функции (10 класс)

Обратные тригонометрические функции
.

Что же такое функция?
Зависимая переменная Соответствие y = f (x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины х сответсвует определенное значение другой величины у. Такое соответствие может быть задано различном образом , например : формулой, графически или таблицей. С помощью функции математически выражаются многообразные количественные закономерности в природе.

Рассмотрим следующие обратные функции:
у = arcsin х у = arccos х у = arctg х у = arcctg х

Обратная функция -
функция, обращающая зависимость, выражаемую данной функцией. Так, если y =f ( x) — данная функция, то переменная х, рассматриваемая как функция переменной у: х = j( y), является обратной по отношению к данной функции у = f ( x). Напр., х = есть обратная функция по отношению к y = x3.

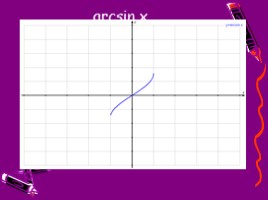
у = arcsin x
Функция y = sin x, рассматриваемая на промежутке [ -П/2 ; П/2] , имеет обратную функцию, которую называют арксинусом и записывают ч у = arcsin х , Свойства этой функции 1) Область определения – промежуток [ -1 ; 1] 2) Множество значений – промежуток [ -П/2 ; П/2] 3) Эта функция нечетная 4) Функция возрастает 5) Функция непрерывна

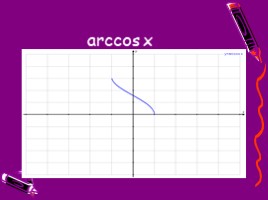
у = arccos x
Функция у = cos x, рассматриваемая на промежутке [0;П], имеет обратную функцию, которую называют арккосинусом и записывают у = arccos х
Свойства этой функции 1) Область определения – промежуток [ -1 ; 1] 2) Множество значений – промежуток [ 0 ; П] 3) Эта функция не является ни четной ни нечетной 4) Функция убывает 5) Функция непрерывна

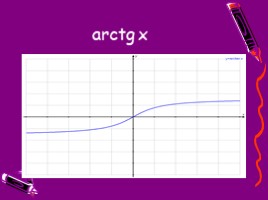
у = arctg x
Функция y = tg x, рассматриваемая на промежутке (-П/2;П/2), имеет обратную функцию, которую называют арктангенсом записывают у = arctg х Свойства этой функции 1) Область определения – вся числовая прямая 2) Множество значений – промежуток (-П/2;П/2) 3) Эта функция является нечетной 4) Функция возрастает 5) Функция непрерывна

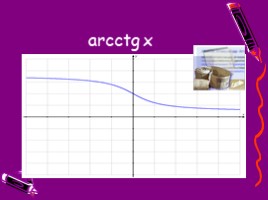
у = arcctg x
Функция Y = ctg x, рассматриваемая на промежутке (0;П), имеет обратную функцию, которую называют арктангенсом и записывают у = arcctg х
Свойства этой функции 1) Область определения – вся числовая прямая 2) Множество значений – промежуток (0;П) 3) Эта функция не является ни четной ни нечетной 4) Функция убывает 5) Функция непрерывна

arcsin x

arccos x

arctg x

arcctg x