Презентация - Свойства и графики Тригонометрических функций

Свойства и графики Тригонометрических функций. х у

Основные вопросы: Функция у sin x , её свойства и график. Функция y cos x , её свойства и график. Функция y tgx , её свойства и график. Функция y ctg x , её свойства и график.

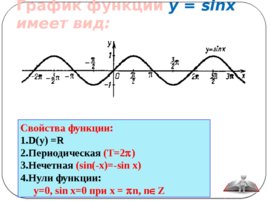
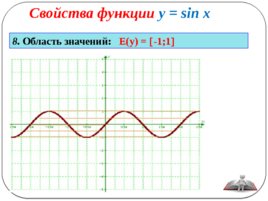
График функции y sinx имеет вид: Свойства функции: D(y) R Периодическая (Т 2 p ) Нечетная (sin(-x) -sin x) Нули функции: у 0, sin x 0 при х p n, n Î Z

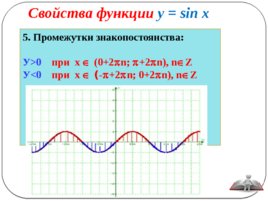
Свойства функции у sin x 5. Промежутки знакопостоянства: У 0 при х Î (0 2 p n; p 2 p n), n Î Z У при x Î ( - p 2 p n; 0 2 p n), n Î Z

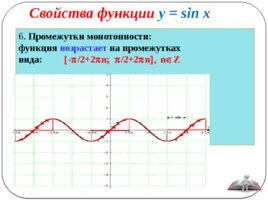
Свойства функции у sin x 6. Промежутки монотонности: функция возрастает на промежутках вида: - p /2 2 p n; p /2 2 p n , n Î Z

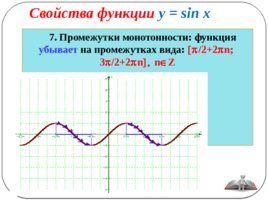
Свойства функции у sin x 7. Промежутки монотонности: функция убывает на промежутках вида: p /2 2 p n; 3 p /2 2 p n , n Î Z

Свойства функции у sin x 8. Область значений: Е(у) -1;1

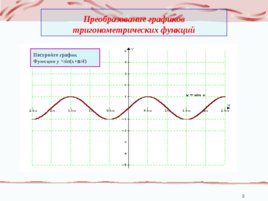
Преобразование графиков тригонометрических функций График функции у f (x в) получается из графика функции у f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс График функции у f (x) а получается из графика функции у f(x) параллельным переносом на (а) единиц вдоль оси ординат

Преобразование графиков тригонометрических функций Постройте график Функции у sin(x p /4)

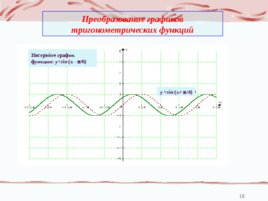
Преобразование графиков тригонометрических функций y sin (x p /4) Постройте график функции: y sin (x - p /6)

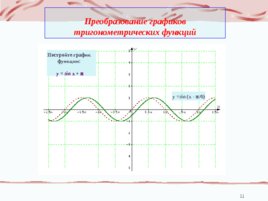
Преобразование графиков тригонометрических функций y sin x p Постройте график функции: y sin (x - p /6)

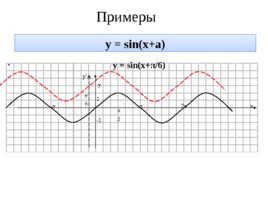
у sin(x a) y sin(x π/6) y 1 -π π 2π х -1 Примеры

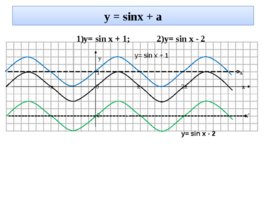
у sinx a 1)y sin x 1; 2)y sin x - 2 y 1 x' -π 0 π 2π x -2 x'' y sin x 1 y sin x - 2

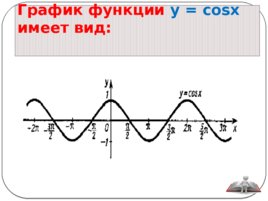
График функции y cosx имеет вид:

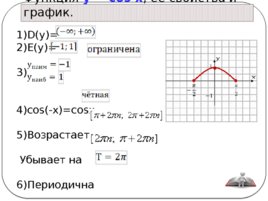
Функция y cos x , её свойства и график. 1)D(y) 2)E(y) 3) 4)cos(-x) cosx 5) Возрастает на Убывает на 6)Периодична

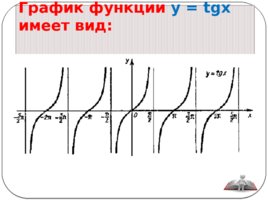
График функции y tgx имеет вид:

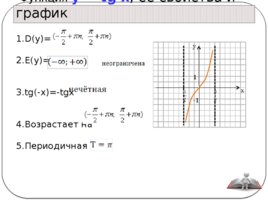
Функция y tg x , её свойства и график 1. D(y) 2. E(y) 3.tg(-x) -tgx 4. Возрастает на 5. Периодичная 1 -1

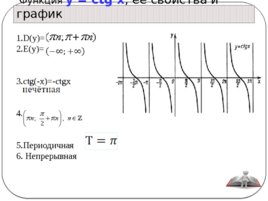
График функции y ctgx имеет вид:

1. D(y) 2. E(y) 3.ctg(-x) -ctgx 4. Убывает на 5. Периодичная 6. Непрерывная Функция y сtg x , её свойства и график

Домашнее задание: