Презентация - Обратные функции. Свойства взаимно обратных функций. х у

Обратные функции. Свойства взаимно обратных функций. х у

Основные вопросы: 1. Функция у arcsin x , её свойства и график. 2. Функция y arсcos x , её свойства и график. 3. Функция y arctgx , её свойства и график. 4. Функция y arcctg x , её свойства и график.

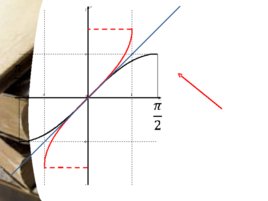
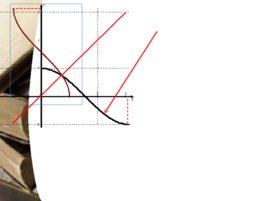
Функция, обратная функции sin x Арксинусом числа а называется число b из - П / 2 ; П / 2 такое, что sin b a. Обозначение: arcsin b a. D (arcsin х) -1;1 Е (arcsin х) - П /2; П /2 Функция у arcsin х нечетная arcsin (-х) - arcsin х Функция у arcsin х непрерывная на -1;1 Функция у arcsinх возрастает на области определения График функции у arcsin х симметричен части графика у sin х при хЄ - П /2; П /2 относительно прямой у х

Функция, обратная функции cos x Арккосинусом числа а называется число b из - 1 ; 1 такое, что соs b a Обозначение: arcсоs b a D (arcсоs х) -1; 1 Е (arcсоs х) 0; П Функция у arcсоs х не является четной и нечетной arcсоs (-х) П -arcсоs х Функция у arcсоs х непрерывная на -1;1 Функция у arcсоs х убывает на области определения График функции у arcсоs х симметричен части графика у соs х при хЄ 0 ; П относительно прямой у х

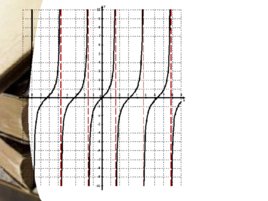
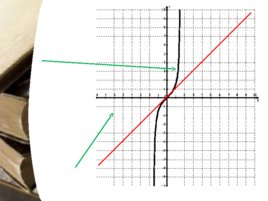
Функция, обратная функции tg x Арктангенсом числа а называется число b из (- П / 2 ; П / 2 ) такое, что tg b a Обозначение: arctg b a. D (arctg х) R Е (arctg х) (- П /2; П /2 ) Функция у arctg х нечетная arctg (-х) - arctg х Функция у arctg х возрастает на области определения График функции у arctg х cимметричен части графика у tg х при хЄ (- П /2; П /2 ) относительно прямой у х

-1 π 0 1 х у

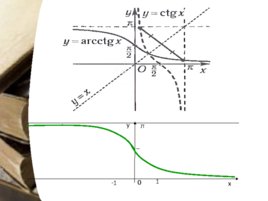
Функция, обратная функции ctg x Арккотангенсом числа а называется число b из (0; П ) такое, что сtg b a Обозначение: arcсtg b a. D (arсctg х) R Е (arсctg х) (0 ; П ) Функция у arсctg х не является четной и нечетной arсctg (-х) П - arcсtg х Функция у arсctg х убывает на области определения График функции у arсctg х cимметричен части графика у сtg х при хЄ (0 ; П ) относительно прямой у х

Преобразование выражений

Уравнения, содержащие обратные тригонометрические функции

Домашнее задание: