Презентация - «Взаимно обратные функции»

«Взаимно обратные функции»

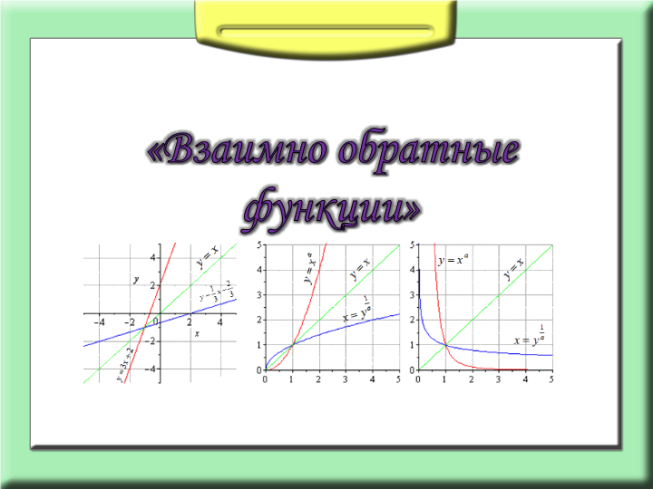
Взаимно обратные функции
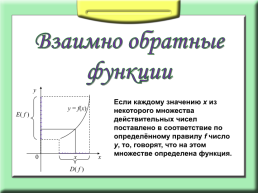
Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определённому правилу f число у, то, говорят, что на этом множестве определена функция.

Задача. у = f (x), х - ? Найти значение х при заданном значении у.
Обратная
Прямая
Задача. у = f (x), у - ? Найти значение у при заданном значении х.
Дано: у = 2х + 3, у (х) = 42 Найти: х Решение: 42 = 2х + 3 2х = 39 х = 19,5 Ответ: у (19,5) = 42
Дано: у = 2х + 3 Найти: у (5) Решение: у (5) = 2 · 5 + 3 = 13 Ответ: у (5) = 13

Если функция у = f ( х ) принимает каждое своё значение у только при одном значении х, то эту функцию называют обратимой.
Пусть у = f(x) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определённое число х из области её определения, такое, что f(x) = y. Это соответствие определяет функцию х от у, которую обозначим х = g(y). Поменяем местами х и у: у = g(x). Функцию у = g(x) называют обратной к функции у = f(x).

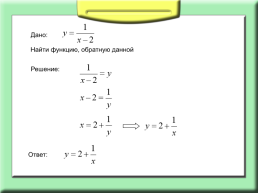
Дано:
Найти функцию, обратную данной
Решение:
Ответ:

у
у
х
х
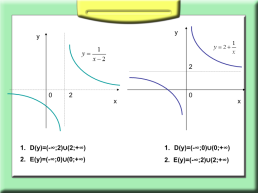
D(у)=(-∞;2)∪(2;+∞) Е(у)=(-∞;0)∪(0;+∞)
D(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)

Возрастающие и убывающие функции называют монотонными.
Теорема: Монотонная функция является обратимой. если функция f возрастает, то обратная к ней функция f -1 также возрастает; если функция f убывает, то обратная к ней функция f -1 также убывает.

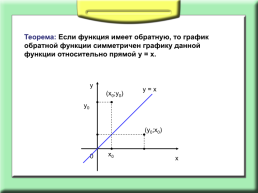
Теорема: Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у = х.
у
у = х
(х0;у0)
у0
(у0;х0)
х0
х

у
у
у=f(x)
y=x2,х<0
у=g(x)
-2
х
х
-2
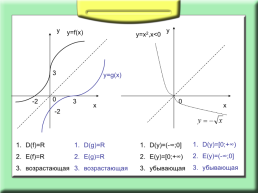
D(y)=[0;+∞) E(y)=(-∞;0] убывающая
D(f)=R E(f)=R возрастающая
D(g)=R E(g)=R возрастающая
D(y)=(-∞;0] E(y)=[0;+∞) убывающая

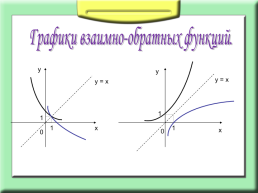
Графики взаимно-обратных функций.
у
у
у = х
у = х
х
х

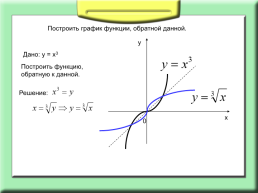
Построить график функции, обратной данной.
у
Дано: у = х3
Построить функцию, обратную к данной.
Решение:
х

Практический приём нахождения формулы функции, обратной к функции y=f(x)
Пример
Алгоритм

Примеры решения задач
Найдите функцию, обратную к функции
Решение
Комментарий

Выполнить задания

Д/з. п.2, стр.185. №574, №575