Презентация - Кривые линии (лекция 6)

Лекция 6 Кривые линии . Основные понятия и определения. Виды кривых линий (плоские и пространственные). Применение кривых линий в архитектуре и строительстве. Геометрическая модель поверхности . Способы образования поверхностей. Классификации поверхностей. Линейчатые поверхности. Нелинейчатые поверхности

Кривые линии. Основные понятия и определения Кривые линии широко применяются в архитектуре и строительстве. По кривым линиям очерчиваются различные пространственные формы- арки, своды и т.п. Кривые линии применяют для образования поверхностей различных архитектурных объектов и конструкций зданий – покрытий в виде оболочек, сводов и куполов, пандусов и винтовых лестниц. Кривые линии могут быть результатом пересечения поверхностей, они могут быть краевыми контурами отсеков поверхностей- оболочек или видимыми и очерковыми контурами поверхностей

Кривые линии в начертательной геометрии рассматриваются как непрерывная совокупность последовательных положений движущейся точки , а также как линия пересечения поверхностей Кривая может быть описана (задана) аналитически, т.е. уравнением , например эллипс, парабола и др. Если образование кривой не имеет строгой закономерности, то она задается графически, например горизонтали в плане местности.

Кривые линии. Основные понятия и определения Если все точки кривой линии лежат в одной плоскости, такая кривая линия называется плоской (окружность, эллипс, парабола). Если все точки кривой линии нельзя совместить с плоскостью, то такая кривая линия называется пространственной (например, винтовые линии)

Свойства проекций кривой В начертательной геометрии кривые линии изучаются по их проекциям. Свойства проекций кривой: проекции кривой линии являются также кривыми линиями Если точка принадлежит кривой линии, то ее проекции принадлежат одноименным проекциям этой кривой Касательная к кривой линии проецируется в касательную к проекции этой кривой, если направление проецирования не параллельно касательной

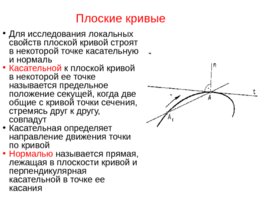
Плоские кривые Для исследования локальных свойств плоской кривой строят в некоторой точке касательную и нормаль Касательной к плоской кривой в некоторой ее точке называется предельное положение секущей, когда две общие с кривой точки сечения, стремясь друг к другу, совпадут Касательная определяет направление движения точки по кривой Нормалью называется прямая, лежащая в плоскости кривой и перпендикулярная касательной в точке ее касания

Свойства точек кривой Точка кривой, в которой можно провести единственную касательную, называется гладкой . Кривая, состоящая только из гладких точек, называется гладкой кривой. Точка кривой называется обыкновенной, если при движении точки по кривой направление ее движения и направление поворота касательной не изменяются Точки, не отвечающие этим условиям, называются особыми

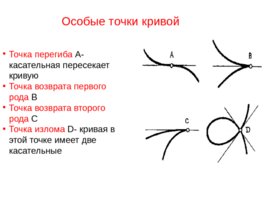
Особые точки кривой Точка перегиба А- касательная пересекает кривую Точка возврата первого рода В Точка возврата второго рода С Точка излома D - кривая в этой точке имеет две касательные

Пространственные кривые Пространственные кривые линии могут иметь самую разнообразную форму. Они могут быть заданы аналитически. Кривые случайного вида задаются графически. Для анализа пространственной кривой необходимо установить самые общие ее свойства, которые изучаются по ее проекциям. Для задания на чертеже пространственной кривой линии и точек, принадлежащих ей, достаточно двух ее проекций – горизонтальной и фронтальной.

Проекции пространственных кривых Наибольшее применение в практике архитектурного проектирования имеют закономерные пространственные кривые , в частности винтовые линии Винтовая линия образуется двойным движением точки – поступательным и вращательным.

Цилиндрическая винтовая линия - гелиса Представляет собой траекторию точки, вращающейся вокруг некоторой прямой и совершающей одновременно равномерное движение вдоль прямой. Фронтальная проекция цилиндрической винтовой линии представляет собой синусоиду Смещение точки вдоль образующей за один оборот называется шагом h винтовой линии При развертывании цилиндрической поверхности в плоскость цилиндрическая винтовая линия изобразится прямой линией. Угол φ , составленный касательной к винтовой линии с плоскостью, перпендикулярной оси, называется углом подъема винтовой линии

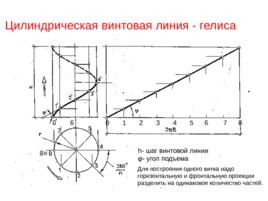
Цилиндрическая винтовая линия - гелиса h - шаг винтовой линии φ - угол подъема 0 1 2 3 4 5 6 7 8 5 6 7 8 Для построения одного витка надо горизонтальную и фронтальную проекции разделить на одинаковое количество частей.

Арх. Ф. Шехтель. Интерьер особняка Дорожинской, 1901 г. В архитектурной практике цилиндрические винтовые линии применяются для образования контуров каркаса и поверхностей винтовых лестниц, винтовых пандусов для въезда автомашин в многоэтажных гаражах, для устройства развязок в двух уровнях на пересечении магистралей.

Коническая винтовая линия Представляет собой траекторию точки, равномерно перемещающейся по образующей прямого кругового конуса и в то же время равномерно вращающейся вместе с образующей вокруг оси. Горизонтальная проекция конической винтовой линии представляет собой спираль Архимеда Проекции каждой точки определяются пересечением соответствующих образующих с проекциями параллелей конуса, плоскости которых смещены по вертикали (в данном примере h /8). Для построения одного витка надо горизонтальную и фронтальную проекции разделить на одинаковое количество частей

Проект памятника III Интернационалу (художник В. Татлин, 1919 г.) Металлическая стержневая наклонная башня высотой 400 м сужается кверху. Динамику всей композиции придают элементы двух конических винтовых линий

Образование и каркас поверхностей В начертательной геометрии поверхность рассматривается как непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону. Такой способ образования поверхностей называется кинематическим

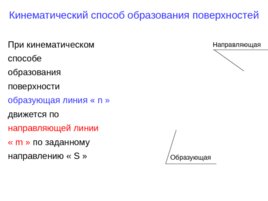
Кинематический способ образования поверхностей Направляющая Образующая При кинематическом способе образования поверхности образующая линия « n » движется по направляющей линии « m » по заданному направлению « S »

Определитель и каркас поверхностей Определитель поверхности – совокупность геометрических элементов и условий, необходимых и достаточных для однозначного задания поверхности в пространстве и на чертеже Поверхность считается заданной, если относительно любой точки пространства однозначно решается вопрос о принадлежности ее к данной поверхности Все поверхности делятся на 2 группы: многогранные и кривые

Многогранные поверхности Многогранной поверхностью называется поверхность, образованная частями (отсеками) пересекающихся плоскостей Отсеки плоскостей называются гранями , а линии их пересечения – ребрами . Совокупность ребер и вершин многогранной поверхности называют сеткой Наиболее распространенные многогранники – призмы и пирамиды Призму, ребра которой перпендикулярны основанию, называют прямой.

Общие положения Направляющая и образующие создают линейчатый каркас поверхности Точка принадлежит поверхности, если она лежит на линии этой поверхности Направляющая « m » может быть: замкнутой или разомкнутой ; плоской или пространственной

Пирамидальная поверхность Определитель – ломаная направляющая « m » и вершина « S » Закон образования : Поверхность образуется движением прямолинейной образующей « а », закрепленной в точке « S » по ломаной направляющей « m ». Направляющая - плоская незамкнутая ломаная линия Проекции ломаной пространственной незамкнутой направляющей

Призматическая поверхность Определитель : ломаная направляющая « m » и заданное направление « S ». Закон образования : Призматическая поверхность образуется движением прямолинейной образующей « n » по ломаной направляющей « m » параллельно заданному направлению « S ». s s 2 s 1 Направляющая- ломаная плоская незамкнутая Проекции ломаной Плоской замкнутой направляющей

Кривые поверхности Кривые поверхности отличаются большим разнообразием форм- от самых простых до сложнейших. Поверхности, полученные на основе геометрического способа образования, отличаются целостностью и структурной четкостью, а также возможностью математического описания и точного отображения на чертеже

Геометрическая форма поверхности определяет не только эстетические качества поверхности. «Несущая способность конструкции – функция ее геометрической формы» (итальянский архитектор и инженер П. Л. Нерви) Современные оболочки способны перекрывать пролеты до 300 м.

Систематизация (классификация) поверхностей По закону движения образующей – поверхности с поступательным движением образующей, с вращательным и винтовым. По виду образующей - поверхности с прямолинейной образующей (линейчатые) и с криволинейной образующей (не линейчатые) По закону изменения формы образующей – с образующей постоянного и переменного вида По признаку развертывания поверхности на плоскость - развертываемые и не развертываемые По способу задания поверхности - аналитическому или графическому (закономерные и незакономерные (графические))

По признаку развертывания поверхности делятся на развертываемые и не развертываемые Развертка : Совмещение поверхности с плоскостью Развертки бывают: Точные – совмещение поверхности с плоскостью без деформаций (многогранные поверхности) Приближенные – имеют место небольшие деформации: растяжения, сжатие, складки (кривые поверхности -линейчатые) Условные – имеют место сильные деформации. Фактически поверхность разрывается на отдельные части (кривые поверхности не линейчатые)

Очертание поверхности Чтобы придать чертежу поверхности наглядность, строят ее очертание – проекцию линии контура поверхности Контуром видимости называется линия, точки которой являются точками касания проецирующих прямых. Проекция контура на плоскости проекций называется очерком поверхности на данной плоскости При изображении поверхности на чертеже проекцию контурной линии называют линией видимости , которая является границей, отделяющей видимую часть поверхности от скрытой, невидимой части данной поверхности на данной плоскости проекций

Очерк Очерк Контур Построение очерка геометрического тела на плоскостях проекций

Линейчатые поверхности Линейчатые поверхности - поверхности, образованные движением прямой образующей в пространстве по определенному закону

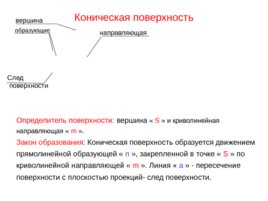
Коническая поверхность Определитель поверхности: вершина « S » и криволинейная направляющая « m ». Закон образования : Коническая поверхность образуется движением прямолинейной образующей « n », закрепленной в точке « S » по криволинейной направляющей « m ». Линия « а » - пересечение поверхности с плоскостью проекций- след поверхности. След поверхности направляющая вершина образующие

Цилиндрическая поверхность Определитель: криволинейная направляющая « m » и заданное направление « s ». Закон образования : Цилиндрическая поверхность образуется движением прямолинейной образующей « n » по криволинейной направляющей « m » параллельно заданному направлению. Линия « а » - пересечение поверхности с плоскостью проекций. а направляющая s s 2 s 1

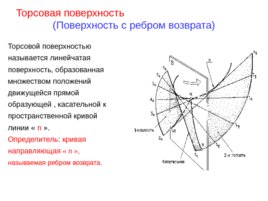
Торсовая поверхность (Поверхность с ребром возврата) Торсовой поверхностью называется линейчатая поверхность, образованная множеством положений движущейся прямой образующей , касательной к пространственной кривой линии « n ». Определитель : кривая направляющая « n », называемая ребром возврата.

Для архитектурно-строительной практики важен случай, когда ребром возврата служит цилиндрическая винтовая линия . Кривая сечения поверхности горизонтальной плоскостью, перпендикулярной оси цилиндра, или горизонтальный след поверхности представляют собой плоскую кривую – эвольвенту , поэтому данную поверхность называют эвольвентной поверхностью или развертываемым геликоидом. Горизонтальная проекция ребра возврата (окружность) является эволютой этой кривой. Эволюта – это множество центров кривизны эвольвенты (точки 1 .12 на окружности)

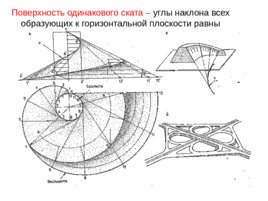
Поверхность одинакового ската – углы наклона всех образующих к горизонтальной плоскости равны

Винтовая поверхность Винтовая поверхность образуется винтовым движением образующей линии. Это совокупность двух движений образующей – поступательного перемещения вдоль оси поверхности и вращательного вокруг оси. Если образующая прямая линия , винтовую поверхность называют геликоидом . Геликоид называют прямым, если образующая составляет с осью поверхности прямой угол. В других случаях геликоид называют наклонным.

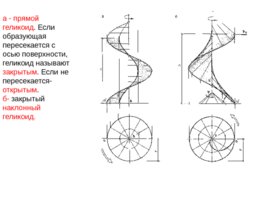
а - прямой геликоид . Если образующая пересекается с осью поверхности, геликоид называют закрытым . Если не пересекается- открытым . б- закрытый наклонный геликоид.

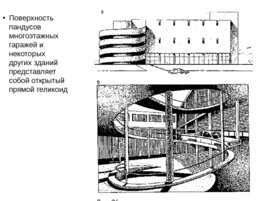
Поверхность пандусов многоэтажных гаражей и некоторых других зданий представляет собой открытый прямой геликоид

Поверхности с плоскостью параллелизма (Поверхности Каталана) Определитель : две направляющих и плоскость параллелизма Закон образования : Прямая образующая движется по двум направляющим одновременно параллельно некоторой плоскости, называемой плоскостью параллелизма В зависимости от вида направляющих различают три вида поверхностей: Цилиндроид : обе направляющие- кривые линии Коноид : одна направляющая кривая, вторая прямая Косая плоскость – две скрещивающиеся прямые направляющие

Цилиндроид Σ 1 Σ 1 Цилиндроид образуется движением прямолинейной образующей ( L ) по двум криволинейным направляющим ( m , n ) параллельно некоторой пло скости параллелизма Σ . Σ 1

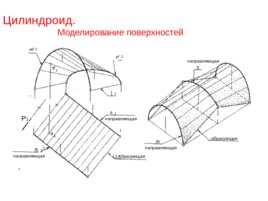
Цилиндроид. Моделирование поверхностей L1- образующая направляющая направляющая - образующая 1 направляющая направляющая 1 1 2 2 2 P 1 1 2

Коноид Коноид образуется движением прямолинейной образующей ( L ) по двум направляющим ( m , n ) , одна из которых – прямая линия, а другая – кривая, параллельно некоторой плоскости параллелизма Σ . Σ 1 Σ 1 Σ 1

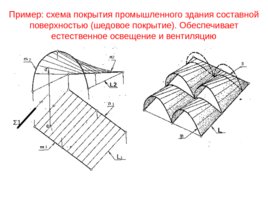
Пример : схема покрытия промышленного здания составной поверхностью (шедовое покрытие). Обеспечивает естественное освещение и вентиляцию L 1 L2 1 1 Σ 1 2 2 2 1 L

Гиперболический параболоид (Косая плоскость) Σ Σ 1 Гиперболический параболоид образуется движением прямолинейной образующей ( L ) по двум прямолинейным направляющим ( m , n ) – (скрещивающимся прямым) параллельно некоторой плоскости параллелизма Σ . m n n 1 m 1 m 2 n 2 m 1 n 1 Σ 1 1

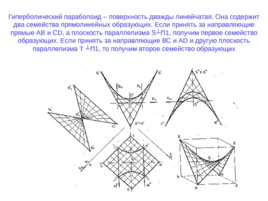
Гиперболический параболоид – поверхность дважды линейчатая. Она содержит два семейства прямолинейных образующих. Если принять за направляющие прямые АВ и С D , а плоскость параллелизма S П 1 , получим первое семейство образующих. Если принять за направляющие ВС и А D и другую плоскость параллелизма Т П 1 , то получим второе семейство образующих

Образующие одного семейства- скрещивающиеся прямые Каждая образующая одного семейства пересекает все образующие другого семейства. Т.о. гиперболический параболоид имеет непрерывный сетчатый каркас из двух семейств пересекающихся образующих. Это свойство придает поверхности большую пространственную жесткость и хорошую технологичность возведения Криволинейные очерки поверхности на фронтальной и профильной проекциях являются параболами

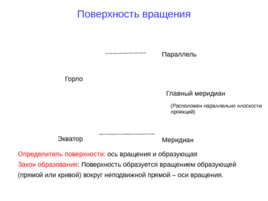
Поверхность вращения Параллель Горло Главный меридиан Меридиан Экватор Определитель поверхности: ось вращения и образующая Закон образования : Поверхность образуется вращением образующей (прямой или кривой) вокруг неподвижной прямой – оси вращения. (Расположен параллельно плоскости проекций)

Сечение поверхности плоскостью, перпендикулярной оси вращения, называется параллелью . Максимальная параллель – экватор . Минимальная- горло поверхности. Сечение поверхности плоскостью вдоль оси – меридианы . Главный меридиан расположен параллельно плоскости проекций (проецируется в натуральную величину на данную плоскость проекций)

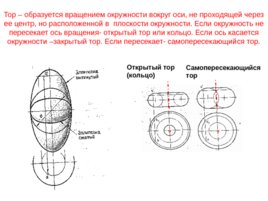
Тор – образуется вращением окружности вокруг оси , не проходящей через ее центр, но расположенной в плоскости окружности. Если окружность не пересекает ось вращения- открытый тор или кольцо. Если ось касается окружности –закрытый тор. Если пересекает- самопересекающийся тор. Открытый тор (кольцо) Самопересекающийся тор

Каркасные поверхности Поверхности, к которым нельзя применить математические или геометрические закономерности, задают сетью линий, заполняющих поверхность и являющихся линейчатым каркасом поверхности. Поверхности, заданные графически семейством линий, принадлежащих поверхности, называют каркасными Каркас поверхности в этом случае называют дискретным в отличие от непрерывного каркаса поверхностей, заданных кинематическим способом. Точки и линии, не лежащие на линиях дискретного каркаса, могут быть построены только приближенно.

Пример : земная поверхность, заданная дискретным каркасом линий уровня- горизонталями и называемая топографической поверхностью. Поверхности такого вида называют графическими, т.к. их можно задать только чертежом.

Построение кривой линии, лежащей на поверхности вращения Гл. меридиан Экватор Гл. меридиан Экватор С 1 α 2 Задача 8.2. стр.40 : Построить горизонтальную проекцию линии АСВ, лежащей на поверхности сферы. Решение: Точка « А » лежит на главном меридиане . А 2 А 1 Точка « С » лежит на экваторе . С 2 С 1 Для построения точки « В » рассекаем сферу плоскостью α , строим параллель радиуса « R » и указываем на ней точку « В » R В 2 В 1

α 2 β 2 Для построения точки « D » рассекаем сферу плоскостью « α », строим парал-лель радиуса « R 1 » и указываем на ней точку « D ». R 1 D 2 D 1 Чтобы построить точку « Е » рассекаем сферу плоскостью « β ». Строим парал - лель радиуса « R 2 » и указываем на ней точку « Е ». R 2 E 2 E 1 На горизонтальной плоскости проекций соединяем проекции точек В 1 , D 1 , С 1 , Е 1 , А 1 . Часть проекции кривой линии В 1 D 1 С 1 - видима, так как лежит выше экватора. Точка « С » - граница видимости. Часть линии А 1 Е 1 С 1 – не видима, так как находится ниже экватора. C 1 С