Презентация - Возведение в степень произведения и степени (урок №40)

7 класс алгебра Возведение в степень произведения и степени (Урок №40)
ГБОШИ РФМЛИ г. Владикавказа Учитель математики высшей категории: Байбус Н. К.

Цели урока:
повторить определение степени, умножение (деление) степеней с одинаковыми основаниями ; изучить правила возведения в степень произведения и степени, закрепить в ходе выполнения упражнений; развивать логическое мышление

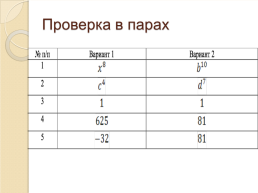
Математический диктант

Проверка в парах

Изучение нового
Представить в виде произведения степеней: Аналогичным свойством обладает любая натуральная степень произведения двух множителей. Запишите формулу. Сделайте вывод.

Изучение нового
Для любых а и в и произвольного натурального числа n Чтобы возвести произведение в степень, достаточно возвести в эту степень каждый множитель и результаты перемножить.

Изучение нового
Представьте в виде степени степень: Аналогичным свойством обладает любая натуральная степень. Запишите формулу. Сделайте вывод.

Изучение нового
Для любого числа а и произвольных натуральных m и n При возведении степени в степень основание оставляют тем же, а показатели перемножают

Отгадать фамилию русского ученого

Этот ученый – М.В. Ломоносов, который сказал:
«Пусть кто-нибудь попробует вычеркнуть из математики степени , и он увидит , что без них далеко не уедешь»

Тренировочные упражнения
а) №430 обращаем внимание на рациональные вычисления №437 начать на доске и закончить с последующей взаимопроверкой б) № 439 в тетрадях, комментируя правилами действий со степенями в) № 441, 142 самостоятельно

Итог урока
Что нового мы узнали? Сформулировать правила: возведение в степень произведения и степени Какие трудности вы испытывали на уроке? Что было легко? Выразите свое настроение при помощи смайлика.

Домашнее задание
Выучить правила: возведение в степень произведения и степени № 391 №394 № 400.

Используемые материалы
Т.М Ерина, Поурочное планирование по алгебре к учебнику Ю. Н. Макарычева и др. «Алгебра, 7 класс », М.: Просвещение, Издание третье, стереотипное, 2011 Алгебра 7 класс, учебник для общеобразовательных школ, под редакцией Теляковского, Москва «Просвещение», 2013 Интернет картинки. http://rebus1.com/index.php?item=rebus_generator&enter=1