Презентация - Признаки параллельности прямых.

11.12.2019 К л а с с н а я р а б о т а. Признаки параллельности прямых.

а
b
аIIb
Определение. Две прямые на плоскости называются параллельными, если они не пересекаются.

Определения
а
Прямая с называется секущей по отношению к прямым а и b, если она пересекает их в двух точках
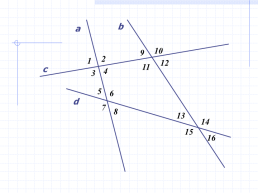
Названия углов
b
накрест лежащие углы (НЛУ):
односторонние углы (ОУ):
соответственные углы (СУ):
с

b
а
c
d

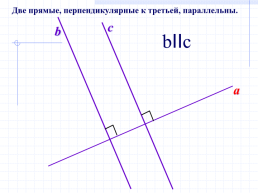
Две прямые, перпендикулярные к третьей, параллельны.
c
b
bIIc
a

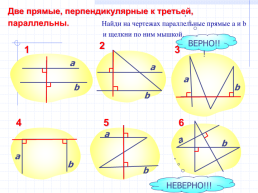
Две прямые, перпендикулярные к третьей, параллельны. Найди на чертежах параллельные прямые a и b и щелкни по ним мышкой.
ВЕРНО!!!
а
а
а
b
b
b
а
а
b
а
b
b
НЕВЕРНО!!!

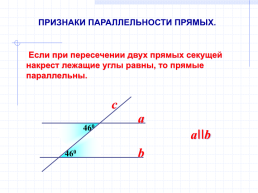
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
c
a
aIIb
b

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Найди на чертежах параллельные прямые a и b и щелкни по ним мышкой.
ВЕРНО!!!
а
а
73023/
b
73023/
b
НЕВЕРНО!!!
а
а
123023/
123021/
b
b

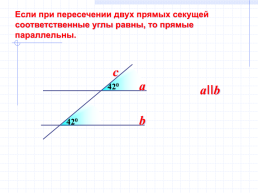
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
c
a
aIIb
b

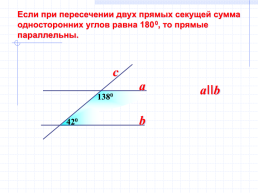
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
c
a
aIIb
b

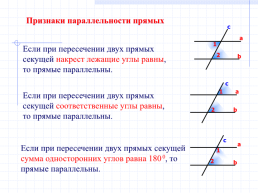
Признаки параллельности прямых
c
а
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
b
c
а
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
b
c
а
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
b

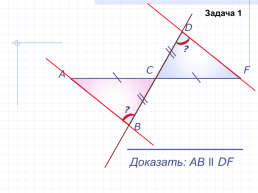
Задача 1
D
?
C
F
A
?
B
Доказать: АB ll DF

Домашнее задание
п. 24 – 25, вопросы 1 – 5 (устно, стр.68). Решить задачи № 186(а,б).

при пересечении двух прямых секущей накрест лежащие углы равны, прямые параллельны.
Если
Условие теоремы
то
Заключение теоремы
Дано: НЛУ 1 = 2. а, b, c- секущая. Доказать: aIIb.
c
А
а
Доказательство: 1 случай Если углы 1 и 2 прямые, то прямые а и b перпендикулярны к прямой АВ, следовательно, aIIb.
b
В

c
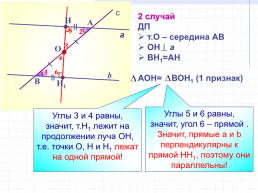
2 случай ДП т.О – середина АВ ОН a BH1=AH АОН= ВОН1 (1 признак)
Н
А
а
О
b
В
Н1
Углы 5 и 6 равны, значит, угол 6 – прямой . Значит, прямые a и b перпендикулярны к прямой НН1, поэтому они параллельны!
Углы 3 и 4 равны, значит, т.Н1 лежит на продолжении луча ОН, т.е. точки О, Н и Н1 лежат на одной прямой!

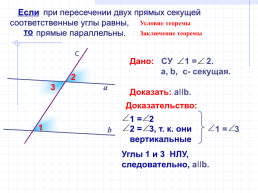
при пересечении двух прямых секущей соответственные углы равны, прямые параллельны.
Если
Условие теоремы
то
Заключение теоремы
c
Дано: СУ 1 = 2. а, b, c- секущая. Доказать: aIIb.
а
Доказательство:
b
Углы 1 и 3 НЛУ, следовательно, aIIb.

при пересечении двух прямых секущей сумма односторонних углов равна 1800, прямые параллельны.
Если
Условие теоремы
то
Заключение теоремы
c
Дано: ОУ 1 + 2 = 1800. а, b, c- секущая. Доказать: aIIb.
а
Доказательство:
b
Углы 1 и 3 НЛУ, следовательно, aIIb.