Презентация - Урок геометрии в 8 классе. Определение подобных треугольников

Урок геометрии в 8 классе
Определение подобных треугольников

Цели урока:
Ввести понятие пропорциональных отрезков и подобных треугольников. Рассмотреть свойство биссектрисы треугольника и показать его применение при решении задач. Развивать навыки самоконтроля, умение анализировать задание, выбирать способы решения.

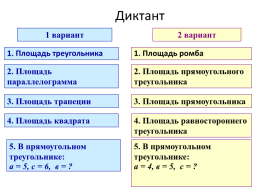
Диктант
1 вариант
2 вариант
1. Площадь треугольника
1. Площадь ромба
2. Площадь параллелограмма
2. Площадь прямоугольного треугольника
3. Площадь трапеции
3. Площадь прямоугольника
4. Площадь квадрата
4. Площадь равностороннего треугольника
5. В прямоугольном треугольнике: а = 5, с = 6, в = ?
5. В прямоугольном треугольнике: а = 4, в = 5, с = ?

Тема урока: Определение подобных треугольников

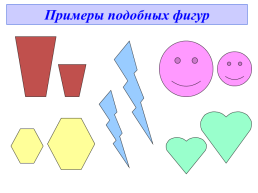
Примеры подобных фигур

1. Пропорциональные отрезки
С
А
В
D
D1
А1
В1
C1
Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1, если отношения их длин равны.

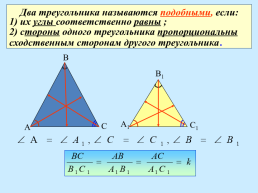
Два треугольника называются подобными, если: 1) их углы соответственно равны ; 2) стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
В
В1
А1
С1
С
А

k – коэффициент подобия
Стороны АВ и А1В1, ВС и В1С1, АС и А1С1 называют сходственными.
Подобие треугольников АВС и А1В1С1 обозначается: Δ АВС ~ Δ А1В1С1

Проверь себя!
1. Верно ли, что у подобных треугольников стороны соответственно равны?
2. Могут ли быть подобными прямоугольный и равнобедренный треугольники? Прямоугольный и тупоугольный треугольники?
3.Могут ли быть подобными треугольник с углом 500 и треугольник с углом 1000? Треугольник с углом 450 и треугольник с углом 1350?
4*. Треугольники АВС и МNK подобны, причем А =  N, В =  K. Назовите сторону, сходственную со стороной MN.

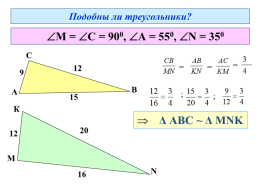
Подобны ли треугольники?
М = С = 900, А = 550, N = 350
С
=
=
=
В
А
;
;
К
 Δ АВС ~ Δ МNK
М
N

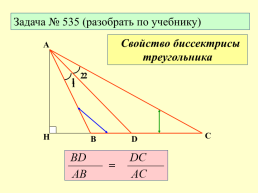
Задача № 535 (разобрать по учебнику)
Свойство биссектрисы треугольника
А
С
H
В
D

Решить: № 536 (а), 534 (а)
Дома: п. 56, 57 (определения), вопросы 1-3, с. 165; № 535 (устно), № 534 (б,в), 536 (б), 538.
Спасибо за урок!