Презентация - Урок геометрии в 7 классе «Треугольники»

Урок геометрии в 7 классе по теме «Треугольники»
Учитель математики Новостроевской средней школы Барышева Т.Н.

«Учиться можно только весело…. Чтобы переваривать знания, надо поглощать их с аппетитом». Анатоль Франс

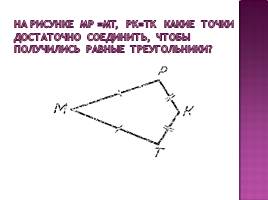
На рисунке МP =MT, PK=TK Какие точки достаточно соединить, чтобы получились равные треугольники?  

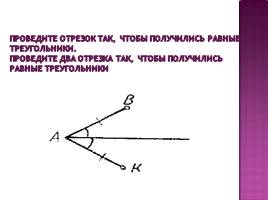
Проведите отрезок так, чтобы получились равные треугольники. Проведите два отрезка так, чтобы получились равные треугольники

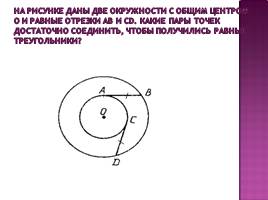
На рисунке даны две окружности с общим центром О и равные отрезки АВ и СD. Какие пары точек достаточно соединить, чтобы получились равные треугольники?

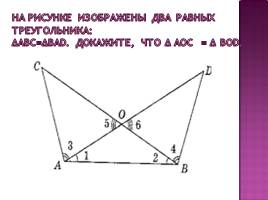
На рисунке изображены два равных треугольника: ∆АВС=∆ВАD. Докажите, что ∆ АОС = ∆ ВОD.

Фалес Милетский - древнегреческий математик
Ему принадлежит открытие следующих теорем: вертикальные углы равны; в равнобедренном треугольнике углы, лежащие при основании, равны; теорема о равенстве двух треугольников по стороне и двум прилежащим к ней углам.
(VI в. до н.э.).

Фалес Милетский Теорема о равенстве двух треугольников
 
Фалес нашёл важное практическое приложение: в гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В, С, (АВ= ВС) и размеченную прямую СК перпендикулярно прямой СА. При появлении корабля на прямой СК находили точку Д такую, чтобы точки Д, В, Е оказывались на одной прямой. Как ясно из чертежа, расстояние на земле СД и является искомым расстоянием до корабля АЕ по воде.

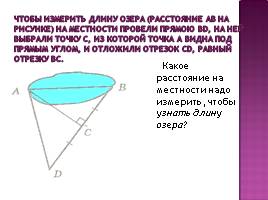
Чтобы измерить длину озера (расстояние АВ на рисунке) на местности провели прямою ВD, на ней выбрали точку C, из которой точка А видна под прямым углом, и отложили отрезок СD, равный отрезку ВC.
Какое расстояние на местности надо измерить, чтобы узнать длину озера?

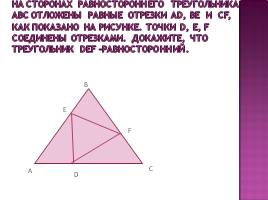
На сторонах равностороннего треугольника АВС отложены равные отрезки AD, BE и CF, как показано на рисунке. Точки D, E, F соединены отрезками. Докажите, что треугольник DEF –равносторонний.
В
А
С
E
F
D

Спасибо!