Слайды и текст этой онлайн презентации
Слайд 2
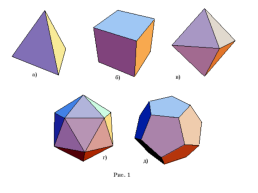
Многогранник, точнее трёхмерный многогранник — совокупность конечного числа плоских многоугольников в трёхмерном евклидовом пространстве, такая, что:
каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым (по этой стороне);
связность: от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним, и т. д.
Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины —вершинами многогранника.
.
Слайд 5
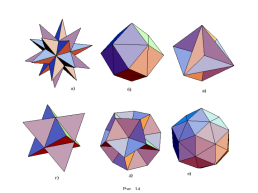
Многогранник называется правильным, если:
- он выпуклый;
- все его грани являются равными правильными многоугольниками;
- в каждой его вершине сходится одинаковое число рёбер.
Слайд 6
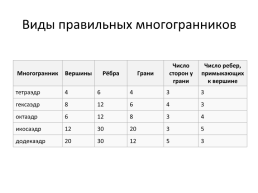
Виды правильных многогранников
Многогранник.Вершины.Рёбра.Грани.Число сторон у грани.Число ребер, примыкающих к вершине
тетраэдр.4.6.4.3.3
гексаэдр.8.12.6.4.3
октаэдр.6.12.8.3.4
икосаэдр.12.30.20.3.5
додекаэдр.20.30.12.5.3
Слайд 7
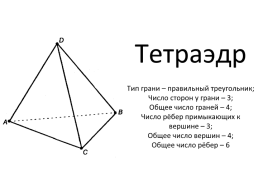
Тетраэдр Тип грани – правильный треугольник; Число сторон у грани – 3; Общее число граней – 4; Число рёбер примыкающих к вершине – 3; Общее число вершин – 4; Общее число рёбер – 6
Слайд 8
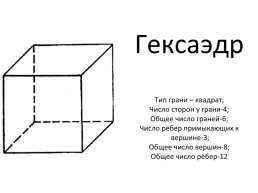
Гексаэдр Тип грани – квадрат; Число сторон у грани-4; Общее число граней-6; Число рёбер примыкающих к вершине-3; Общее число вершин-8; Общее число рёбер-12
Слайд 9
Октаэдр Тип грани-правильный треугольник; Число сторон у грани -3; Общее число граней -8; Число рёбер примыкающих к вершине -4; Общее число вершин -6; Общее число рёбер -12
Слайд 10
Икосаэдр Тип грани –правильный треугольник; Число сторон у грани -3; Общее число граней -20; Число рёбер примыкающих к вершине -5; Обще число вершин -12; Общее число рёбер-30
Слайд 11
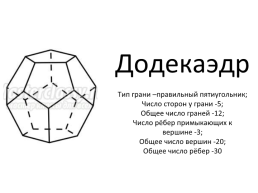
Додекаэдр Тип грани –правильный пятиугольник; Число сторон у грани -5; Общее число граней -12; Число рёбер примыкающих к вершине -3; Общее число вершин -20; Общее число рёбер -30
 Понятие многогранника. Правильные многогранники.
Понятие многогранника. Правильные многогранники. Что за чудо эти многогранники?
Что за чудо эти многогранники? Стереометрия на ЕГЭ: тела вращения, многогранники
Стереометрия на ЕГЭ: тела вращения, многогранники Проект «Полуправильные многогранники»
Проект «Полуправильные многогранники» Платоновы тела - Правильные выпуклые многогранники
Платоновы тела - Правильные выпуклые многогранники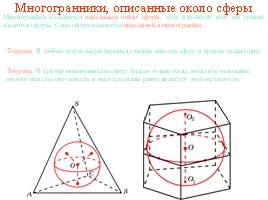 Многогранники, описанные около сферы
Многогранники, описанные около сферы Правильные многогранники.. 1
Правильные многогранники.. 1