Презентация - Стереометрия на ЕГЭ: тела вращения, многогранники

Стереометрия на ЕГЭ: тела вращения, многогранники

План занятия
1. Цилиндр
2. Конус
3. Шар
4. Комбинация тел вращения и многогранников звание графика

№ 1. В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
Решение. Объём детали равен объёму вытесненной ею жидкости. Объём вытесненной жидкости равен 9/12 исходного объёма:
Ответ: 1500.

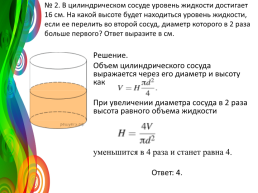
№ 2. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.
Решение. Объем цилиндрического сосуда выражается через его диаметр и высоту как При увеличении диаметра сосуда в 2 раза высота равного объема жидкости уменьшится в 4 раза и станет равна 4. Ответ: 4.

№ 3. Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Решение. Пусть объём первого цилиндра равен  где R1, 2 — радиусы оснований цилиндров, H1, 2 — их высоты. По условию
Выразим объём второго цилиндра через объём первого:
Ответ : 9

№ 4. Площадь боковой поверхности цилиндра равна 2? , а диаметр основания — 1. Найдите высоту цилиндра.
Решение : Площадь боковой поверхности цилиндра находится по формуле: Значит
Ответ : 2

№ 5. Площадь боковой поверхности цилиндра равна 2?, а высота — 1. Найдите диаметр основания.
Решение: Площадь боковой поверхности цилиндра находится по формуле: Значит Ответ : 2

№ 6. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на ? .
Решение: Площадь осевого сечения цилиндра равна S=2rh, так как это прямоугольник. Тогда для площади боковой поверхности имеем: Ответ : 4

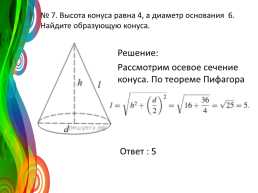
№ 7. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Решение: Рассмотрим осевое сечение конуса. По теореме Пифагора Ответ : 5

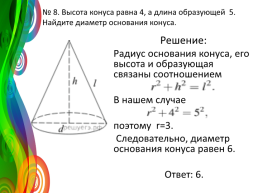
№ 8. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Решение: Радиус основания конуса, его высота и образующая связаны соотношением В нашем случае поэтому r=3. Следовательно, диаметр основания конуса равен 6. Ответ: 6.

№ 9. Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
Решение. Рассмотрим осевое сечение конуса. По теореме Пифагора Ответ: 4.

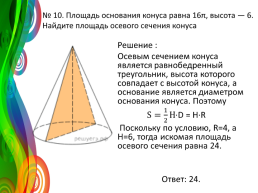
№ 10. Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса
Решение : Осевым сечением конуса является равнобедренный треугольник, высота которого совпадает с высотой конуса, а основание является диаметром основания конуса. Поэтому ·D = H·R Поскольку по условию, R=4, а H=6, тогда искомая площадь осевого сечения равна 24. Ответ: 24.

№ 11. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на ? .
Решение: Площадь поверхности складывается и Радиус основания найдем по теореме Пифагора для треугольника, образованного высотой, образующей и радиусом: Тогда площадь поверхности равна Ответ : 144

№ 12. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Решение: Из условия имеем: Значит, в прямоугольном треугольнике, образованном высотой, образующей и радиусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Следовательно, угол между образующей конуса и плоскостью основания равен 60°. Ответ : 60

№ 13. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
Решение: Площадь боковой поверхности конуса равна где C — длина окружности основания, а l — образующая. При увеличении образующей в 3 раза площадь боковой поверхности конуса увеличится в 3 раза. Ответ : 3

№ 14. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
Решение: Площадь боковой поверхности конуса равна S= ?rl, где r — радиус окружности в основании, а l — образующая. Поэтому при уменьшении радиуса основания в 1,5 раза при неизменной величине образующей площадь боковой поверхности тоже уменьшится в 1,5 раза. Ответ : 1,5

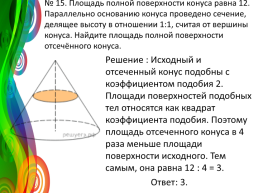
№ 15. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
Решение : Исходный и отсеченный конус подобны с коэффициентом подобия 2. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия. Поэтому площадь отсеченного конуса в 4 раза меньше площади поверхности исходного. Тем самым, она равна 12 : 4 = 3. Ответ: 3.

№ 16. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение: Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 70⋅8=560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости. Ответ: 490.

№ 17. Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
Решение: Объём конуса равен где  S — площадь основания, а  h — высота конуса. При уменьшении высоты в 3 раза объем конуса также уменьшится в 3 раза. Ответ: 3.

№ 18. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?
Решение: Объём конуса равен где  S — площадь основания,  h —высота конуса, а  r — радиус основания. При увеличении радиуса основания в 1,5 раза объем конуса увеличится в 2,25 раза. Ответ: 2,25.

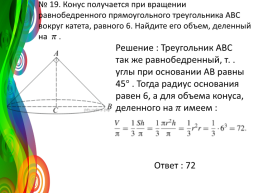
№ 19. Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 6. Найдите его объем, деленный на ? .
Решение : Треугольник ABC — так же равнобедренный, т. к. углы при основании AВ равны 45° . Тогда радиус основания равен 6, а для объема конуса, деленного на ? имеем : Ответ : 72

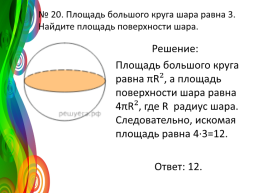
№ 20. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Решение: Площадь большого круга равна πR², а площадь поверхности шара равна 4πR², где R — радиус шара. Следовательно, искомая площадь равна 4·3=12. Ответ: 12.

№ 21. Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение : Площадь поверхности шара выражается через его радиус формулой S=4?r², поэтому при увеличении радиуса вдвое площадь увеличится в 2·2 = 4раза. Ответ: 4

№ 22. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Решение: Из условия находим Ответ: 10

№ 23. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Решение : Объём шара вычисляется по формуле Поэтому cумма объёмов трёх шаров равна Следовательно, искомый радиус равен 12. Ответ: 12.

№ 24. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Решение: Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна Площадь поверхности шара радиуса r равна S=4?r² , то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12. Ответ : 12

№ 25. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Решение : Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен Ответ : 4

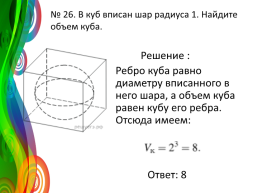
№ 26. В куб вписан шар радиуса 1. Найдите объем куба.
Решение : Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем: Ответ: 8

№ 27. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Решение : Объем цилиндра равен произведению площади основания на высоту, а объем конуса равен одной трети произведения площади основания на высоту. Поскольку они имеют общее основание и высоту, объем цилиндра в три раза больше объема конуса. Ответ: 75.

№ 28. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Решение: Объём конуса в 4 раза меньше: Ответ : 7

№ 29. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Решение : Площадь боковой поверхности прямой призмы равна произведению периметра основания на боковое ребро. Боковое ребро равно высоте цилиндра. В основании призмы лежит квадрат, его сторона равна диаметру вписанного круга. Поэтому Поскольку по условию площадь боковой поверхности равна 48, искомая высота равна 3. Ответ : 3

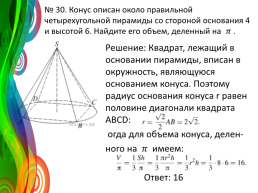
№ 30. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на ? .
Решение: Квадрат, лежащий в основании пирамиды, вписан в окружность, являющуюся основанием конуса. Поэтому радиус основания конуса r равен половине диагонали квадрата ABCD:  Тогда для объема конуса, делен- ного на ? имеем: Ответ: 16

Спасибо за внимание!