Презентация - Решение стереометрических задач на ЕГЭ

Решение стереометрических задач на ЕГЭ
Многогранники

План занятия

№ 1. Диагональ куба равна . Найдите его объём.

№ 2. Площадь поверхности куба равна 24. Найти объём куба.

№ 3. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Решение. Пусть длина третьего ребра, исходящего из той же вершины, равна x, тогда площадь поверхности параллелепипеда даётся формулой,   По условию площадь поверхности равна 16, тогда  Длина диагонали прямоугольного параллелепипеда равна квадратному корню из суммы квадратов его измерений, поэтому Ответ: 3.

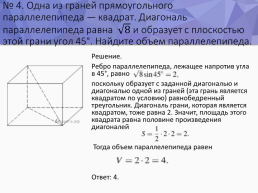
№ 4. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол 45°. Найдите объем параллелепипеда.
Решение. Ребро параллелепипеда, лежащее напротив угла в 45°, равно поскольку образует с заданной диагональю и диагональю одной из граней (эта грань является квадратом по условию) равнобедренный треугольник. Диагональ грани, которая является квадратом, тоже равна 2. Значит, площадь этого квадрата равна половине произведения диагоналей Тогда объем параллелепипеда равен Ответ: 4.

№ 5. Объём параллелепипеда равен 4,5. Найдите объём треугольной пирамиды
Решение. Искомый объем равен разности объемов параллелепипеда и четырех пирамид, основания которых являются гранями данной треугольной пирамиды. Объём каждой из этих пирамид равен одной трети произведения площади основания на высоту, а площадь основания вдвое меньше площади основания параллелепипеда: Ответ : 1,5

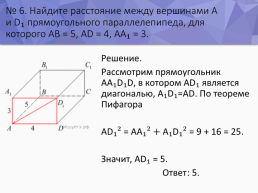
№ 6. Найдите расстояние между вершинами А и D₁ прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA₁ = 3.
Решение. Рассмотрим прямоугольник AA₁D₁D, в котором AD₁ является диагональю, A₁D₁=AD. По теореме Пифагора AD₁² = AA₁² + A₁D₁² = 9 + 16 = 25. Значит, AD₁ = 5. Ответ: 5.

№ 7. Найдите угол ABD₁ прямоугольного параллелепипеда, для которого AB=5, AD=4, AA₁=3. Дайте ответ в градусах.
Решение. В прямоугольнике AA₁D₁D отрезок AD₁ является диагональю, A₁D₁=AD. По теореме Пифагора Прямоугольный треугольник ABD₁ равнобедренный: AB=AD₁=5, значит, его острые углы равны 45° Ответ: 45.

№ 8. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB = 3, AD = 5, AA₁ = 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C₁.
Решение. Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение ABC₁D₁ — параллелограмм. Кроме того, ребро AB перпендикулярно граням AA₁D₁D и BB₁C₁C. Поэтому углы D₁AB и ABC₁ — прямые. Поэтому сечение ABC₁D₁ — прямоугольник.
Из прямоугольного треугольника AD₁D найдем AD₁: Тогда площадь прямоугольника ABC₁D₁ равна: AB ⋅ AD₁ = 3 ⋅ 13 = 39. Ответ:39.

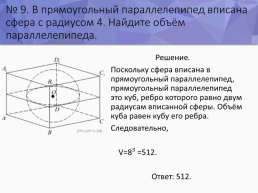
№ 9. В прямоугольный параллелепипед вписана сфера с радиусом 4. Найдите объём параллелепипеда.
Решение. Поскольку сфера вписана в прямоугольный параллелепипед, прямоугольный параллелепипед — это куб, ребро которого равно двум радиусам вписанной сферы. Объём куба равен кубу его ребра. Следовательно, V=8³ =512. Ответ: 512.

№ 10. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см³  воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см³.
Решение. Объём детали равен объёму вытесненной ею жидкости. Объём вытесненной жидкости равен 2/25 исходного объёма: Ответ: 184.

№ 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
Решение. Объем призмы равен произведению площади ее основания на высоту и выражается через сторону основания а и высоту Н формулой Поэтому а значит, при увеличении стороны а в 4 раза знаменатель увеличится в 16 раз, то есть высота уменьшится в 16 раз и будет равна 80 : 16 = 5 см. Ответ: 5.

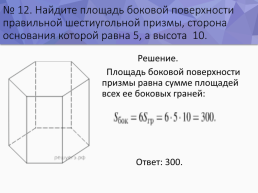
№ 12. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Решение. Площадь боковой поверхности призмы равна сумме площадей всех ее боковых граней: Ответ: 300.

№ 13. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Решение. Площадь основания отсеченной части меньше площади основания всей призмы в 4 раза (так как и высота и основание треугольника уменьшились в 2 раза). Высота призмы осталась прежней, следовательно, объем уменьшился в 4 раза, т.е 32 : 4 = 8 Ответ: 8.

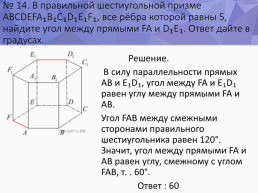
№ 14. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все рёбра которой равны 5, найдите угол между прямыми FA и D₁E₁. Ответ дайте в градусах.
Решение. В силу параллельности прямых AB и E₁D₁, угол между FA и E₁D₁ равен углу между прямыми FA и AB. Угол FAB между смежными сторонами правильного шестиугольника равен 120°. Значит, угол между прямыми FA и AB равен углу, смежному с углом FAB, т. е. 60°. Ответ : 60

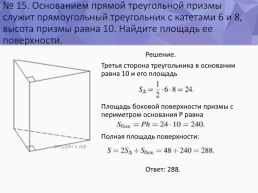
№ 15. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Решение. Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна Полная площадь поверхности: Ответ: 288.

№ 16. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками A и E₁.
Решение. Рассмотрим прямоугольный треугольник AA₁E₁. По теореме Пифагора Угол между сторонами правильного шестиугольника равен 120 градусов . По теореме косинусов Значит, Ответ: 2.

№ 17. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите тангенс угла AD₁D.
Решение. Рассмотрим прямоугольный треугольник ADD₁, катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне: AD=2. Поскольку DD₁=1 имеем: Ответ: 2.

№ 18. В правильной четырехугольной пирамиде SABCD точка O – центр основания, S – вершина, SO=15, BD=16. Найдите боковое ребро SA.
Решение. В правильной пирамиде вершина проецируется в центр основания, следовательно, SO является высотой пирамиды. тогда по теореме Пифагора
Ответ : 17

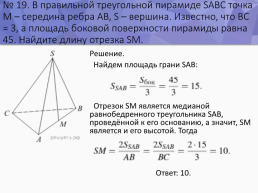
№ 19. В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
Решение. Найдем площадь грани SAB: Отрезок SM является медианой равнобедренного треугольника SAB, проведённой к его основанию, а значит, SM является и его высотой. Тогда Ответ: 10.

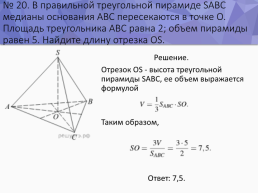
№ 20. В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 5. Найдите длину отрезка OS.
Решение. Отрезок OS - высота треугольной пирамиды SABC, ее объем выражается формулой Таким образом, Ответ: 7,5.

№ 21. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Решение. Площадь пирамиды равна Полупериметр основания p = 20, апофему h найдем по теореме Пифагора: Тогда площадь поверхности пирамиды Ответ: 340.

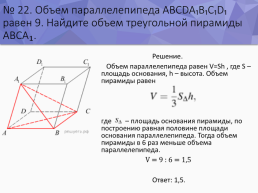
№ 22. Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 9. Найдите объем треугольной пирамиды ABCA₁.
Решение. Объем параллелепипеда равен V=Sh , где S – площадь основания, h – высота. Объем пирамиды равен где – площадь основания пирамиды, по построению равная половине площади основания параллелепипеда. Тогда объем пирамиды в 6 раз меньше объема параллелепипеда. V = 9 : 6 = 1,5 Ответ: 1,5.

№ 23. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Решение. В основании правильной четырехугольной пирамиды лежит квадрат. Пусть его центр — точка О, по теореме Пифагора находим Тогда длина диагонали основания равна 16. Площадь квадрата равна половине произведения его диагоналей, поэтому она равна 128. Следовательно, для объема пирамиды имеем: Ответ: 256.

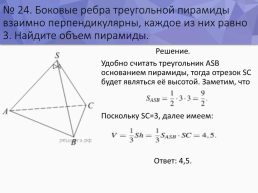
№ 24. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Решение. Удобно считать треугольник ASB основанием пирамиды, тогда отрезок SC будет являться её высотой. Заметим, что Поскольку SC=3, далее имеем: Ответ: 4,5.

№ 25. Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 16. У второй пирамиды высота в 2 раза больше, а сторона основания в 1,5 раза больше, чем у первой. Найдите объём второй пирамиды.
Решение. Объём пирамиды вычисляется по формуле Следовательно, отношение объёмов пирамид: Значит, объём второй пирамиды: 16 · 4,5 = 72. Ответ: 72.

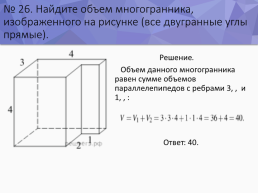
№ 26. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение. Объем данного многогранника равен сумме объемов параллелепипедов с ребрами 3, 3, 4 и 1, 1, 4: Ответ: 40.

№ 27. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение. Объем данного многогранника равен разности объемов параллелепипедов с ребрами 3, 3, 4 и 1, 1, 2: Ответ: 34.

Спасибо за внимание!