Презентация - Платоновы тела - Правильные выпуклые многогранники

Правильные выпуклые многогранники
Платоновы тела

Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл

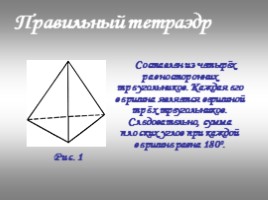
Правильный тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180º.
Рис. 1

Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240º.
Правильный октаэдр
Рис. 2

Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300º.
Рис. 3

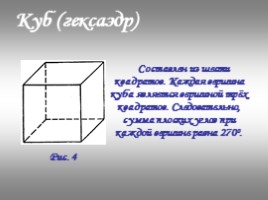
Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270º.
Куб (гексаэдр)
Рис. 4

Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324º.
Рис. 5

пришли из Древней Греции, в них указывается число граней: «эдра»  грань; «тетра»  4; «гекса»  6; «окта»  8; «икоса»  20; «додека»  12.
Названия многогранников

Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.). Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени. Икосаэдр – как самый обтекаемый – воду. Куб – самая устойчивая из фигур – землю. Октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим. Это была одна из первых попыток ввести в науку идею систематизации.
Правильные многогранники в философской картине мира Платона

«Космический кубок» Кеплера
Кеплер предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, к который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Такая модель Солнечной системы (рис. 6) получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта. Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говориться о кубах средних расстояний от Солнца.
Модель Солнечной системы И. Кеплера
Рис. 6

Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение в интересной научной гипотезе, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли (рис. 7). Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.
Икосаэдро- додекаэдровая структура Земли
Икосаэдро-додекаэдровая структура Земли
Рис. 7

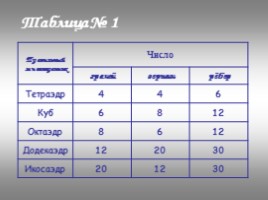
Правильный многогранник Число Число Число
Правильный многогранник граней вершин рёбер
Тетраэдр 4 4 6
Куб 6 8 12
Октаэдр 8 6 12
Додекаэдр 12 20 30
Икосаэдр 20 12 30
Таблица № 1

Правильный многогранник Число Число
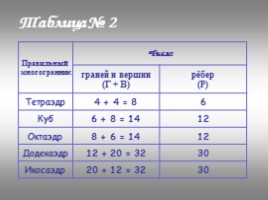
Правильный многогранник граней и вершин (Г + В) рёбер (Р)
Тетраэдр 4 + 4 = 8 6
Куб 6 + 8 = 14 12
Октаэдр 8 + 6 = 14 12
Додекаэдр 12 + 20 = 32 30
Икосаэдр 20 + 12 = 32 30
Таблица № 2

Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В = Р + 2
Формула Эйлера
Число граней плюс число вершин минус число рёбер в любом многограннике равно 2. Г + В  Р = 2

Сальвадор Дали
«Тайная вечеря»

Правильные многогранники и природа
Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр (рис. 8). Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи. Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба. При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2]  12H2O), монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения.
Феодария (Circjgjnia icosahtdra)
Рис. 8

Определите количество граней, вершин и рёбер многогранника, изображённого на рисунке 9. Проверьте выполнимость формулы Эйлера для данного многогранника.
Задача
Рис. 9