Презентация - Аксиомы стереометрии

Аксиомы стереометрии

Содержание:
1.Понятия стереометрии 2. Изображение плоскости 3.Аксиомы стереометрии 4.Следствия из аксиом стереометрии

Система аксиом стереометрии состоит из аксиом планиметрии и трех аксиом стереометрии . В аксиомах стереометрии выражены основные свойства неопределяемых понятий: точки, прямой, плоскости и расстояния. Плоскости - это фигуры, на которых выполняется планиметрия и для которых верны аксиомы стереометрии. Пространство - это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей. Стереометрия – раздел геометрии, в котором изучаются свойства фигур в пространстве

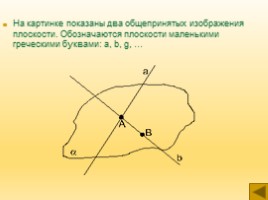
На картинке показаны два общепринятых изображения плоскости. Обозначаются плоскости маленькими греческими буквами: a, b, g, ...

Аксиома 1
Существует хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек. а
а

Аксиома 2
Через любые две различные точки проходит одна и только одна прямая.
А
В

Аксиома 3
Прямая, проходящая через две различные точки плоскости, лежит в этой плоскости
А
В
а

Аксиома 4
Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
А
В
С
а

Аксиома 5
Если две различные плоскости имеют общую точку, то их пересечение есть прямая, которая проходит через эту точку.
А
а
β
с

Аксиома 6
Для любых двух точек А и В имеется неотрицательная величина, называемая расстоянием от А до В. Расстояние от В до А равно нулю в том и только в том случае, если точки А и В совпадают.
А
В
А
В

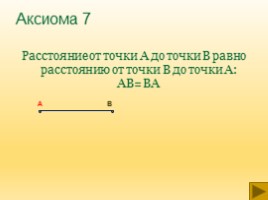
Аксиома 7
Расстояние от точки А до точки В равно расстоянию от точки В до точки А: АВ=ВА
А
В

Аксиома 9
Для каждой плоскости выполняются известные из планиметрии аксиомы порядка, подвижности плоскости и параллельных прямых.

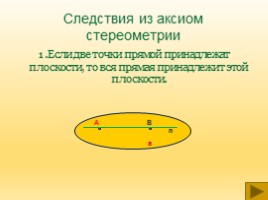
Следствия из аксиом стереометрии
1.Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
А
В
n
а

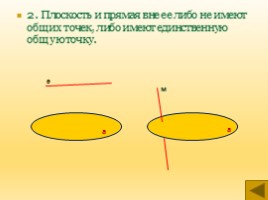
2. Плоскость и прямая вне ее либо не имеют общих точек, либо имеют единственную общую точку.
е
а
а
м