Презентация - Применение признаков подобия треугольников к решению практических задач

Применение признаков подобия треугольников к решению практических задач
Андреева Т.В.

В школе мы довольно подробно изучаем геометрические построения с помощью циркуля и линейки и решаем много задач. А как решить такие же задачи на местности? Ведь невозможно вообразить себе такой огромный циркуль, который мог бы очертить окружность школьного стадиона или линейку для разметки дорожек парка.  На практике картографам для составления карт, геодезистам для того, чтобы размечать участки на местности, например, для закладки фундамента дома, приходится использовать специальные методы.

ФАЛЕС (ок. 625 – ок. 547 до н. э.), древнегреческий мыслитель, родоначальник античной философии и науки, основатель милетской школы. Стал первым, кто ввел в математику принцип математического доказательства, доказал несколько теорем геометрии.

Фалесу приписывается греческими писателями ещё решение двух геометрических задач практического характера, из которых одна состояла в определении расстояния до корабля на море от Милетской гавани, а другая — в определении высоты пирамиды по длине её тени.

В солнечный день он поставил свой посох там, где оканчивалась тень от пирамиды. Затем он показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха.

Измерение высоты предмета с помощью тени
B
F
A
C
D
E

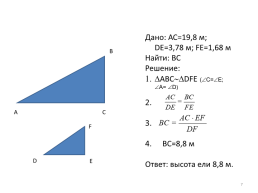
Дано: АС=19,8 м; DE=3,78 м; FE=1,68 м Найти: ВС Решение: АВСDFE (С=Е; А= D) BC=8,8 м Ответ: высота ели 8,8 м.
B
A
C
F
D
E

Измерение высоты предмета с помощью зеркала
E
зеркало
В
A
D
С

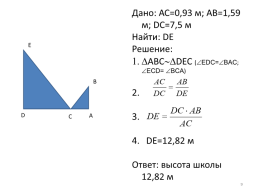
Дано: АС=0,93 м; АВ=1,59 м; DC=7,5 м Найти: DE Решение: АВСDEC (EDC=BAC; ECD= BCA) DE=12,82 м Ответ: высота школы 12,82 м
E
B
D
A
C

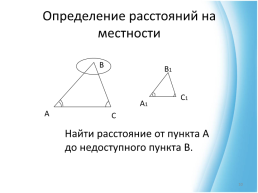
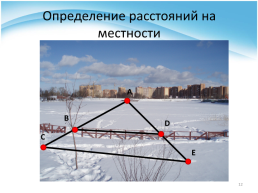
Определение расстояний на местности
Найти расстояние от пункта А до недоступного пункта В.

B
А
C
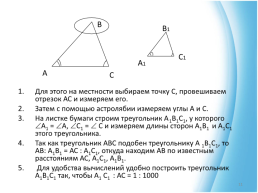
Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябии измеряем углы А и С. На листке бумаги строим треугольник А1В1С1, у которого А1 = А, С1 =  С и измеряем длины сторон А1В1 и А1С1 этого треугольника. Так как треугольник АВС подобен треугольнику А1В1С1, то АВ: А1В1 = АС : А1С1, откуда находим АВ по известным расстояниям АС, А1С1, А1В1. Для удобства вычислений удобно построить треугольник А1В1С1 так, чтобы А1 С1 : АС = 1 : 1000

Определение расстояний на местности
A
B
D
C
E

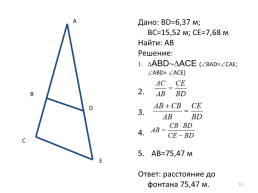
Дано: BD=6,37 м; BC=15,52 м; CE=7,68 м Найти: AB Решение: АВDACE (BAD=CAE; ABD= ACE) AB=75,47 м Ответ: расстояние до фонтана 75,47 м.
A
B
D
C
E

Спасибо за внимание!