Презентация - Тождества. Тождественные преобразования выражений

Тождества. Тождественные преобразования выражений.
7 класс.
Коняхина М.В., учитель математики

Найдем значение выражений при х=5 и у=4
3(х+у)=3(5+4)=3*9=27 3х+3у=3*5+3*4=27 Найдем значение выражений при х=6 и у=5 3(х+у)=3(6+5)=3*11=33 3х+3у=3*6+3*5=33

ВЫВОД:
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных значения выражений 3(х+у) и 3х+3у равны. 3(х+у) = 3х+3у

Рассмотрим теперь выражения 2х+у и 2ху.
при х=1 и у=2 они принимают равные значения: 2х+у=2*1+2=4 2ху=2*1*2=4 при х=3, у=4 значения выражений разные 2х+у=2*3+4=10 2ху=2*3*4=24

ВЫВОД:
Выражения 3(х+у) и 3х+3у являются тождественно равными, а выражения 2х+у и 2ху не являются тождественно равными. Определение: Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.

ТОЖДЕСТВО
Равенство 3(х+у) и 3х+3у верно при любых значениях х и у. Такие равенства называются тождествами.   Определение: Равенство, верное при любых значениях переменных, называется тождеством. Тождествами считают и верные числовые равенства. С тождествами мы уже встречались.

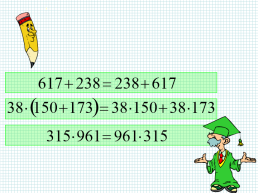
Тождествами являются равенства, выражающие основные свойства действий над числами.
a + b = b + a ab = ba (a + b) + c = a + (b + c) (ab)c = a(bc) a(b + c) = ab + ac

Можно привести и другие примеры тождеств:
а + 0 = а а * 1 = а а + (-а) = 0 а * (-b) = - ab а-b = a + (-b) (-a) * (-b) = ab
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.

Чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть;
Пример 1. Приведем подобные слагаемые 5х +2х-3х=х(5+2-3)=4х

Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки;
Пример 2. Раскроем скобки в выражении 2а + (b-3c) = 2a + b – 3c

Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки.
Пример 3. Раскроем скобки в выражении а – (4b – с) = a – 4b + c

Домашнее задание: п. 5, №91, 97, 99
Спасибо за урок!