Презентация - Преобразование графиков

Преобразование графиков
Учитель математики ГБОУ СОШ №339 Павлова Любовь Васильевна

виды преобразований графиков

7 класс

8 класс

9 класс

Систематизация темы “Преобразование графиков”

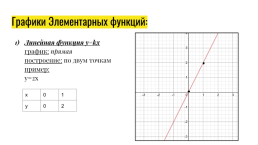
Графики Элементарных функций:
Линейная функция y=kx график: прямая построение: по двум точкам пример: y=2x
x.0.1
y.0.2

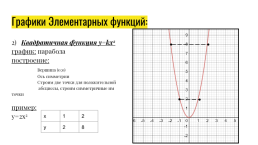
Графики Элементарных функций:
2) Квадратичная функция y=kx2 график: парабола построение: Вершина (0;0) Ось симметрии Строим две точки для положительной абсциссы, строим симметричные им точки пример: y=2x2
x.1.2
y.2.8

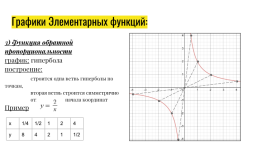
Графики Элементарных функций:
3) Функция обратной пропорциональности график: гипербола построение: строится одна ветвь гиперболы по точкам, вторая ветвь строится симметрично относительно начала координат Пример
x.1/4.1/2.1.2.4
y.8.4.2.1.1/2

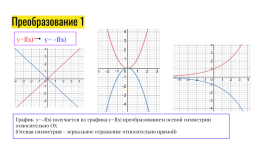
Преобразование 1
y=f(x) y= -f(x)
График y=-f(x) получается из графика y=f(x) преобразованием осевой симметрии относительно OX (Осевая симметрия - зеркальное отражение относительно прямой)

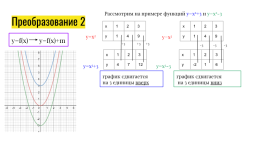
Рассмотрим на примере функций y=x2+3 и y=x2-3
Преобразование 2
x.1.2.3
y.1.4.9
x.1.2.3
y.1.4.9
y=x2
y=x2
y=f(x) y=f(x)+m
+3
+3
+3
-3
-3
-3
x.1.2.3
y.4.7.12
x.1.2.3
y.-2.1.6
y=x2+3
y=x2-3
график сдвигается на 3 единицы вверх
график сдвигается на 3 единицы вниз

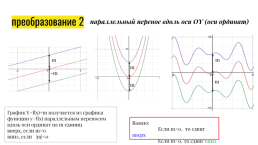
преобразование 2
параллельный перенос вдоль оси ОY (оси ординат)
m
m
m
-m
m
m
График Y=f(x)+m получается из графика функции y=f(x) параллельным переносом вдоль оси ординат на m единиц вверх, если m>0 вниз, если |m|<0
Важно: Если m>0, то сдвиг вверх Если m<0, то сдвиг вниз

преобразование 2
параллельный перенос вдоль оси ОY (оси ординат)
Ордината точки пересечения графика функции с осью OY и есть свободный член многочлена

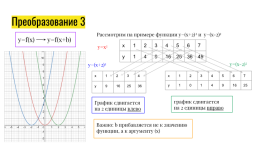
Преобразование 3
Рассмотрим на примере функции y=(x+2)2 и y=(x-2)2
y=f(x) y=f(x+b)
x.1.2.3.4.5.6.7
y.1.4.9.16.25.36.49
y=x2
y=(x-2)2
y=(x+2)2
x.1.2.3.4
y.9.16.25.36
x.1.2.3.4.5.6.7
y.1.0.1.4.9.16.25
график сдвигается на 2 единицы вправо
График сдвигается на 2 единицы влево
Важно: b прибавляется не к значению функции, а к аргументу (x)

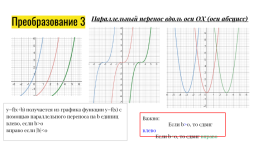
Параллельный перенос вдоль оси OX (оси абсцисс)
Преобразование 3
y=f(x+b) получается из графика функции y=f(x) с помощью параллельного переноса на b единиц влево, если b>0 вправо если |b|<0
Важно: Если b>0, то сдвиг влево Если b<0, то сдвиг вправо

Преобразование 4
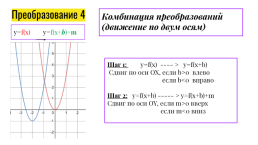
Комбинация преобразований (движение по двум осям)
y=f(x) y=f(x+b)+m
Шаг 1: y=f(x) ---- > y=f(x+b) Сдвиг по оси OX, если b>0 влево если b<0 вправо Шаг 2: y=f(x+b) ----- > y=f(x+b)+m Сдвиг по оси OY, если m>0 вверх если m<0 вниз

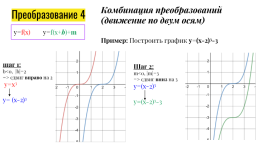
Комбинация преобразований (движение по двум осям)
Преобразование 4
y=f(x) y=f(x+b)+m
Пример: Построить график y=(x-2)3-3
шаг 1: b<0, |b|=2 => сдвиг вправо на 2 y=x3 y= (x-2)3
Шаг 2: m<0, |m|=3 => сдвиг вниз на 3 y=(x-2)3 y=(x-2)3-3

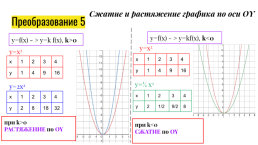
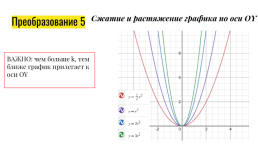
Сжатие и растяжение графика по оси OY
Преобразование 5
y=f(x) - > y=kf(x), k<0
y=f(x) - > y=k f(x), k>0
y=x2
y=x2
x.1.2.3.4
y.1.4.9.16
x.1.2.3.4
y.1.4.9.16
y=½ x2
y=2x2
x.1.2.3.4
y.2.1/2.9/2.8
x.1.2.3.4
y.2.8.18.32
при k>0 РАСТЯЖЕНИЕ по OY
при k<0 СЖАТИЕ по OY

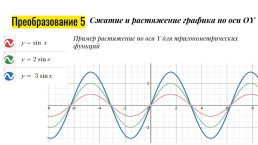
Преобразование 5
Сжатие и растяжение графика по оси OY
Пример растяжение по оси Y для тригонометрических функций

Сжатие и растяжение графика по оси OY
Преобразование 5
ВАЖНО: чем больше k, тем ближе график прилегает к оси OY

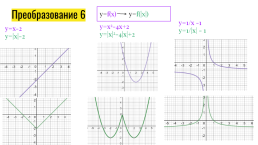
Преобразование 6
y=f(x) y=f(|x|)
y=1/x -1 y=1/|x| - 1
y=x2-4x+2 y=|x|2-4|x|+2
y=x-2 y=|x|-2

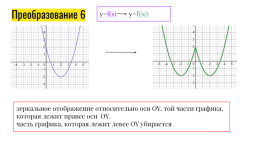
Преобразование 6
y=f(x) y=f(|x|)
зеркальное отображение относительно оси OY, той части графика, которая лежит правее оси OY. часть графика, которая лежит левее OY убирается

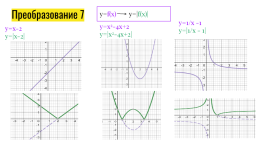
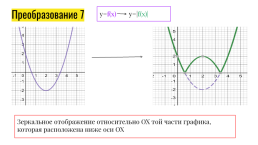
Преобразование 7
y=f(x) y=|f(x)|
y=1/x -1 y=|1/x - 1|
y=x2-4x+2 y=|x2-4x+2|
y=x-2 y=|x-2|

Преобразование 7
y=f(x) y=|f(x)|
Зеркальное отображение относительно OX той части графика, которая расположена ниже оси OX

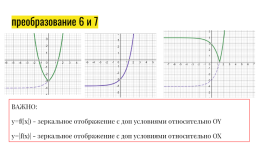
преобразование 6 и 7
ВАЖНО: y=f(|x|) - зеркальное отображение с доп условиями относительно OY y=|f(x)| - зеркальное отображение с доп условиями относительно OX