Презентация - Системы счисления

1
Системы счисления

2
Системы счисления
§ 9. Системы счисления

3
Что такое система счисления?
Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также соответствующие правила выполнения операций с этими числами.
Счёт на пальцах:
Унарная (лат. unus – один) – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)
только натуральные числа запись больших чисел – длинная (1 000 000?)

4
Египетская десятичная система
лотос
– 1 – 10 – 100
– 1000 – 10000 – 100000
– 1000000
черта
палец
хомут
человек
верёвка
лягушка
= ?
=1235
2014 = ?

5
Непозиционные системы счисления
Непозиционная система счисления: значение цифры не зависит от её места в записи числа.
унарная египетская десятичная римская славянская и другие…
«Пираты XX века»

6
Римская система счисления
I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев), X – 10 (две ладони), L – 50, C – 100 (Centum), D – 500 (Demimille), M – 1000 (Mille)
Спасская башня Московского Кремля

7
Римская система счисления
Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только одна!) стоит слева от старшей, она вычитается из суммы (частично непозиционная!) Примеры: MDCXLIV =
+ 500
+ 100
– 10
+ 50
– 1
+ 5
= 1644
2389 = 2000 + 300 + 80 + 9
M M
CCC
LXXX
IX
2389 = M M C C C L X X X I X

8
Римская система счисления
MCDLXVII =
MMDCXLIV =
MMMCCLXXII =
CMXXVIII =

9
Римская система счисления
3768 =
2983 =
1452 =
1999 =

10
Римская система счисления
только натуральные числа (дробные? отрицательные?) для записи больших чисел нужно вводить новые цифры сложно выполнять вычисления

11
Славянская система счисления
алфавитная система счисления (непозиционная)
Часы Суздальского Кремля

12
Системы счисления
§ 10. Позиционные системы счисления

13
Определения
Позиционная система: значение цифры определяется ее позицией в записи числа. Алфавит системы счисления — это используемый в ней набор цифр. Основание системы счисления — это количество цифр в алфавите (мощность алфавита). Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.

14
Формы записи чисел
развёрнутая форма записи числа
разряды
3 2 1 0
6 3 7 5
= 6·103 + 3·102 + 7·101 + 5·100
Схема Горнера:
6 3 7 5 = ((610 + 3)10 + 7)10 + 5
для вычислений не нужно использовать возведение в степень удобна при вводе чисел с клавиатуры, начиная с первой

15
Перевод в десятичную систему
Через развёрнутую запись:
=1
разряды: 3 2 1 0
12345 = 153 + 252 + 351 + 450 = 194
основание системы счисления
разряды: 3 2 1 0
a3a2a1a0 = a3p 3 + a2p 2 + a1p 1 + a0p 0
Через схему Горнера:
12345 = ((15 + 2)5 + 3)5 + 4 = 194
a3a2a1a0 = ((a3p + a2)p + a1)p + a0

16
Перевод из десятичной в любую
194 = 12345 = ((15 + 2)5 + 3)5 + 4
делится на 5
остаток от деления на 5
a3a2a1a0 = ((a3p + a2)p + a1)p + a0
a3a2a1 = (a3p + a2)p + a1
остаток от деления на p
частное от деления на p

17
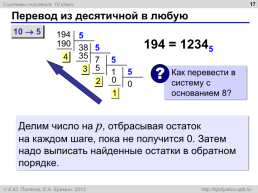
Перевод из десятичной в любую
10  5
194 = 12345
Делим число на p, отбрасывая остаток на каждом шаге, пока не получится 0. Затем надо выписать найденные остатки в обратном порядке.

18
Задачи
Задача: в некоторой системе счисления число 71 записывается как «56x»? Определите основание системы счисления X.
71 = 56X
в записи есть цифра 6, поэтому X > 6 переводим правую часть в десятичную систему решаем уравнение
1 0
56x
= 5·X1 + 6·X0
= 5·X + 6
71 = 5·X + 6
X = 13

19
Задачи
Задача: в некоторой системе счисления число 71 записывается как «155x»? Определите основание системы счисления X.
71 = 155X
в записи есть цифра 5, поэтому X > 5 переводим правую часть в десятичную систему решаем уравнение
2 1 0
155x
= 1·X2 + 5·X1 + 5·X0
= X2 + 5·X + 5
71 = X2 + 5·X + 5
X = 6
X = -11

20
Задачи
Задача: найдите все основания систем счисления, в которых запись десятичного числа 24 оканчивается на 3.
24 = k·X + 3
21 = k·X
X = 3, 7, 21

21
Задачи
Задача: найдите все десятичные числа, не превосходящие 40, запись которых в системе счисления с основанием 4 оканчивается на 11.
N = k·42 + 1·4 + 1 = k·16 + 5
При k =0, 1, 2, 3, … получаем
N = 5, 21, 37, 53, …

22
Задачи
Задача: Все 5-буквенные слова, составленные из букв А, О и У, записаны в алфавитном порядке. Вот начало списка: 1. ААААА 2. ААААО 3. ААААУ 4. АААОА 5. … Найдите слово, которое стоит на 140-м месте от начала списка.
1. 00000 2. 00001 3. 00002 4. 00010 5. …
в троичной системе!
на 1-м месте: 0 на 140-м месте: 139
139 = 120113

23
Дробные числа
0,6375 = 6·0,1 + 3·0,01 + 7·0,001 + 5·0,0001
Развёрнутая форма записи:
разряды: -1 -2 -3 -4
0, 6 3 7 5 = 6·10-1 + 3·10-2 + 7·10-3 + 5·10-4
0, 1 2 3 45 = 1·5-1 + 2·5-2 + 3·5-3 + 4·5-4
перевод в десятичную систему
Схема Горнера:
0, 6375 = 10-1·(6 + 10-1·(3 + 10-1·(7 + 10-1·5)))
0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4)))
перевод в десятичную систему

24
Дробные числа: из десятичной в любую
0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4)))
5·(0,12345)= 1 + 5-1·(2 + 5-1·(3 + 5-1·4))
целая часть
дробная часть
0,a1a2a3a4 = p-1(a1 + p-1(a2 + p-1(a1 + p-1 a0)))
p(0,a1a2a3a4) = a1 + p-1(a2 + p-1(a1 + p-1 a0))

25
Дробные числа: из десятичной в любую
0,9376
10  5
Вычисления.Целая часть.Дробная часть
0,9376  5 = 4,688.4.0,688
0,688  5 = 3,44.3.0,44
0,44  5 = 2,2.2.0,2
0,2  5 = 1.1.0
0,9376 = 0,43215
0,3
10  5

26
Дробные числа: из десятичной в любую
10  6
25,375
= 25 + 0,375

27
Системы счисления
§ 11. Двоичная система счисления

28
Двоичная система
Основание (количество цифр): 2 Алфавит: 0, 1
10  2
19 = 100112
система счисления
2  10
4 3 2 1 0
разряды
= 1·24 + 0·23 + 0·22 + 1·21 + 1·20 = 16 + 2 + 1 = 19

29
Метод подбора
10  2
наибольшая степень двойки, которая меньше или равна заданному числу
1024.512.256.128.64.32.16.8.4.2.1
210.29.28.27.26.25.24.23.22.21.20
+ 1
77 = 64 +
+ 8 + …
+ 4 + …
Разложение по степеням двойки: 77 = 26 + 23 + 22 + 20
77 = 126 + 025 + 024 + 123 +122 +021 + 1 20
6 5 4 3 2 1 0
разряды
77 = 10011012

30
Перевод из двоичной в десятичную
6 5 4 3 2 1 0
разряды
10011012 = 26 + 23 + 22 + 20
= 64 + 8 + 4 + 1 = 77
Схема Горнера:
Разряд..Вычисления.Результат
6.1.1.1
5.0.12+0.2
4.0.22+0.4
3.1.42+1.9
2.1.92+1.19
1.0.192+0.38
0.1.382+1.77

31
Арифметические операции
сложение
вычитание
0+0=0 0+1=1 1+0=1 1+1=102 1 + 1 + 1 = 112
0-0=0 1-1=0 1-0=1 102-1=1
перенос
заём


0 1 1 102
0 102
1 0 1 1 02 + 1 1 1 0 1 12
1 0 0 0 1 0 12 – 1 1 0 1 12

32
Арифметические операции

33
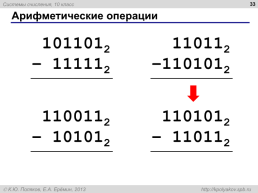
Арифметические операции

34
Арифметические операции
умножение
деление
1 0 1 0 12 – 1 1 12
1 1 12
1 0 1 0 12  1 0 12
1 1 12 – 1 1 12
1 0 1 0 12 + 1 0 1 0 12
1 1 0 1 0 0 12

35
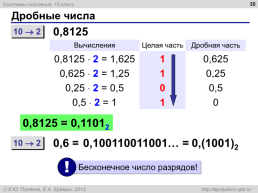
Дробные числа
0,8125
10  2
Вычисления.Целая часть.Дробная часть
0,8125  2 = 1,625.1.0,625
0,625  2 = 1,25.1.0,25
0,25  2 = 0,5.0.0,5
0,5  2 = 1.1.0
0,8125 = 0,11012
0,6 =
0,100110011001… =
0,(1001)2
10  2

36
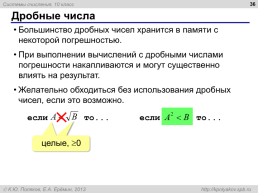
Дробные числа
Большинство дробных чисел хранится в памяти с некоторой погрешностью. При выполнении вычислений с дробными числами погрешности накапливаются и могут существенно влиять на результат. Желательно обходиться без использования дробных чисел, если это возможно.
если то...
если то...

37
Двоичная система счисления
нужны только устройства с двумя состояниями надёжность передачи данных при помехах компьютеру проще выполнять вычисления (умножение сводится сложению и т.п.)
длинная запись чисел: 1024 = 100000000002 запись однородна (только 0 и 1)

38
Системы счисления
§ 12. Восьмеричная система счисления

39
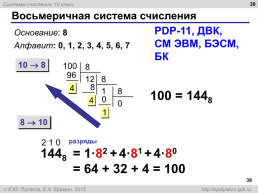
Восьмеричная система счисления
PDP-11, ДВК, СМ ЭВМ, БЭСМ, БК
Основание: 8 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
10  8
100 = 1448
8  10
2 1 0
разряды
= 1·82 + 4·81 + 4·80 = 64 + 32 + 4 = 100

40
Примеры
134 =
75 =
1348 =
758 =

41
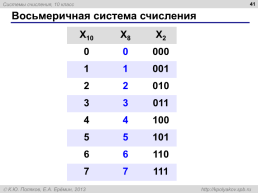
Восьмеричная система счисления
X10.X8.X2
0.0.000
1.1.001
2.2.010
3.3.011
4.4.100
5.5.101
6.6.110
7.7.111

42
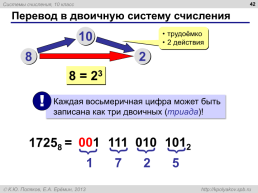
Перевод в двоичную систему счисления
трудоёмко 2 действия
8 = 23
17258 =
{
{
{
{
1 7 2 5

43
Примеры
34678 =
21488 =
73528 =
12318 =

44
Перевод из двоичной в восьмеричную
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной восьмеричной цифрой:
001 001 011 101 1112
Ответ: 10010111011112 = 113578

45
Примеры
1011010100102 =
111111010112 =
11010110102 =

46
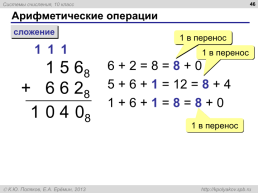
Арифметические операции
сложение
1 в перенос
1 в перенос
1 5 68 + 6 6 28
6 + 2 = 8 = 8 + 0 5 + 6 + 1 = 12 = 8 + 4 1 + 6 + 1 = 8 = 8 + 0
1 в перенос

47
Примеры

48
Арифметические операции
вычитание
заём


4 5 68 – 2 7 78
(6 + 8) – 7 = 7 (5 – 1 + 8) – 7 = 5 (4 – 1) – 2 = 1
заём

49
Примеры

50
Системы счисления
§ 13. Шестнадцатеричная система счисления

51
Шестнадцатеричная система счисления
Основание: 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
A, 10
B, 11
C, 12
D, 13
E, 14
F 15
10  16
444 = 1BC16
С
B
16  10
2 1 0
разряды
B
C
1BC16
= 1·162 + 11·161 + 12·160 = 256 + 176 + 12 = 444

52
Примеры
1C516 =
171 =
206 =
22B16 =

53
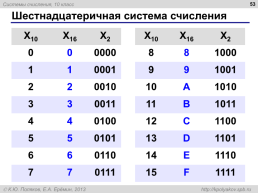
Шестнадцатеричная система счисления
X10.X16.X2..X10.X16.X2
0.0.0000..8.8.1000
1.1.0001..9.9.1001
2.2.0010..10.A.1010
3.3.0011..11.B.1011
4.4.0100..12.C.1100
5.5.0101..13.D.1101
6.6.0110..14.E.1110
7.7.0111..15.F.1111

54
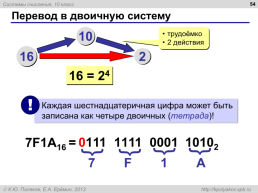
Перевод в двоичную систему
трудоёмко 2 действия
16 = 24
7F1A16 =
{
{
{
{
7 F 1 A

55
Примеры
C73B16 =
2FE116 =

56
Перевод из двоичной системы
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной шестнадцатеричной цифрой:
0001 0010 1110 11112
E
F
Ответ: 10010111011112 = 12EF16

57
Примеры
10101011010101102 =
1111001101111101012 =
1101101101011111102 =

58
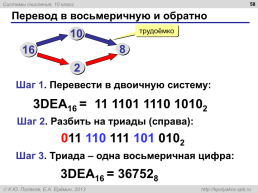
Перевод в восьмеричную и обратно
трудоёмко
Шаг 1. Перевести в двоичную систему:
3DEA16 =
11 1101 1110 10102
Шаг 2. Разбить на триады (справа):
011 110 111 101 0102
Шаг 3. Триада – одна восьмеричная цифра:
3DEA16 = 367528

59
Примеры
A3516 =
7658 =

60
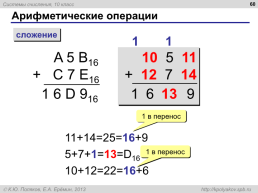
Арифметические операции
сложение
A 5 B16 + C 7 E16
10 5 11 + 12 7 14
1 6 D 916
1 в перенос
11+14=25=16+9 5+7+1=13=D16 10+12=22=16+6
1 в перенос

61
Примеры
С В А16 + A 5 916
F D В16 + A B C16

62
Арифметические операции
заём
вычитание


С 5 B16 – A 7 E16
12 5 11 – 10 7 14
1 D D16
заём
(11+16)–14=13=D16 (5 – 1)+16 – 7=13=D16 (12 – 1) – 10 = 1

63
Примеры
1 В А16 – A 5 916

64
Системы счисления
§ 14. Другие системы счисления

65
Задача Баше о наборе гирь
Как с помощью 4-х гирь взвесить от 0 до 40 кг?
+ 1 гиря на правой чашке 0 гиря снята – 1 гиря на левой чашке
Веса гирь – степени числа 3: 1 кг, 3 кг, 9 кг, 27 кг Пример: 27 кг + 9 кг + 3 кг + 1 кг = 40 кг

66
Троичная уравновешенная система
ЭВМ «Сетунь» (1958) , Н.П. Брусенцов Основание: 3 Алфавит: («-1»), 0, 1 Для N разрядов: всего 3N значений: 0 + по [3N/2] положительных и отрицательных чисел
уравновешенная система
–4..= (–1)31 + (–1)30
–3.0.= (–1)31 + 030
–2.1.= (–1)31 + 130
–1.0.= 031 + (–1)30
0.0 0.= 031 + 030
1.0 1.= 031 + 130
2.1.= 131 + (–1)30
3.1 0.= 131 + 030
4.1 1.= 131 + 130
и положительные, и отрицательные числа для изменения знака нужно поменять знаки у всех цифр запись короче, чем в двоичной системе
нужны элементы с тремя состояниями

67
Двоично-десятичная система (ДДС)
Десятичные цифры, закодированные в двоичном коде. Вinary coded decimal (BCD).
9024,19 = 1001 0000 0010 0100, 0001 1001ДДС 9 0 2 4 1 9
101010011,01111ДДС = = 0001 0101 0011, 0111 1000ДДС = 153,78
легко переводить в десятичную систему просто умножать и делить на 10 конечные десятичные дроби записываются точно (аналог ручных расчётов)
длиннее, чем двоичная запись сложнее арифметические операции
Использование – в калькуляторах.

68
Конец фильма
ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург kpolyakov@mail.ru ЕРЕМИН Евгений Александрович к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь eremin@pspu.ac.ru

69
Источники иллюстраций
http://www.najboljamamanasvetu.com http://www.tissot.ch http://www.mindmeister.com http://www.antiqueclocksshop.com/ http://en.wikipedia.org http://ru.wikipedia.org авторские материалы