Слайды и текст этой онлайн презентации
Слайд 1
муниципальное автономное общеобразовательное учреждение Гимназия №6 г.о. Красноармейск
Учитель математики:
Дымова Валентина Викторовна
Слайд 2
Проверка домашней работы.
Дана функция у = ax2 + bx + c. Для какого из графиков заданы функции
1. Функция задана формулой у = х2 + 6х +5
2. Функция задана формулой у = -х2 + 6х – 5
3. Функция задана формулой у = -(х-3)2 + 4
4. Функция задана формулой у = (х + 3)2 – 4
5. Множество значений функции [-4; ∞)
6. Множество значений функции ( -∞; 4]
7. Функция возрастает на промежутке (-∞; 2]
8. Функция убывает на промежутке (-∞; 4]
9. Максимальное значение функции у = 4
10. Минимальное значение функции у = -4
11. Функция возрастает на множестве значений аргумента [-2; ∞)
12.Функция убывает на множестве значений аргумента [4; ∞)
Слайд 3
ЕНЕЕРИШ АТВНСВЕНРЕ
Слайд 4
ЕНЕЕРИШ АТВНСВЕНРЕ
РЕШЕНИЕ НЕРАВЕНСТВ
Слайд 5
Решение неравенств
Цели урока:
1.Образовательная: продолжить формирование системы знаний о способах решения неравенств различного уровня сложности. Обобщить и систематизировать сведения о неравенствах, способах их решения.
2. Развивающая: углубить и обобщить знания и умения решать неравенства различных типов, неравенства с модулем и системы неравенств
3.Воспитательная: воспитывать умение работать с имеющейся информацией, уважительное отношение к товарищу, положительные мотивы к учебе, добросовестное отношение к труду, дисциплинированность.
Слайд 6
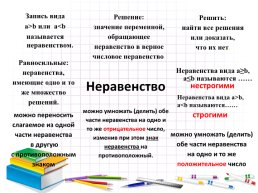
Запись вида
а>b или аРешение:
значение переменной, обращающее неравенство в верное числовое неравенство.
Решить:
найти все решения или доказать,
что их нет.
Равносильные:
неравенства, имеющие одно и то же множество решений.
Неравенства вида а≥b, а≤b называются ……
Неравенство
нестрогими
Неравенства вида а>b, аможно умножать (делить) обе части неравенства на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
строгими
можно переносить слагаемое из одной части неравенства
в другую
с противоположным знаком
можно умножать (делить) обе части неравенства
на одно и то же положительное число
Слайд 10
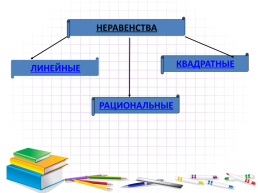
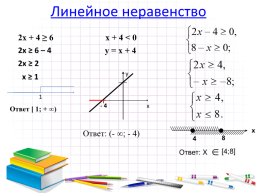
Линейное неравенство
х + 4 ˂ 0
у = х + 4
Ответ: (- ∞; - 4)
Слайд 11
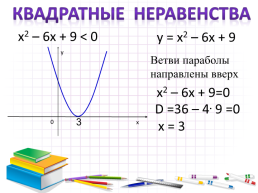
Квадратные неравенства
х2 – 6х + 9 < 0
у = х2 – 6х + 9
Ветви параболы направлены вверх
х2 – 6х + 9=0
D =36 – 4. 9 =0
х = 3
Слайд 12
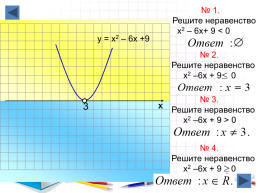
№ 1.
Решите неравенство
х2 – 6х+ 9 < 0
у = х2 – 6х +9
№ 2.
Решите неравенство
х2 –6х + 9 0
№ 3.
Решите неравенство
х2 –6х + 9 > 0
х
№ 4.
Решите неравенство
х2 –6х + 9 0
Слайд 13
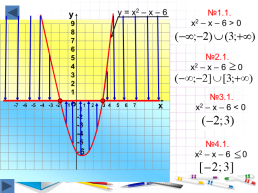
у = х2 – х – 6
№1.1.
х2 – х – 6 > 0
у
9
8
7
6
5
4
3
2
1
№2.1.
№3.1.
х2 – х – 6 < 0
о
х
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
№4.1.
Слайд 14
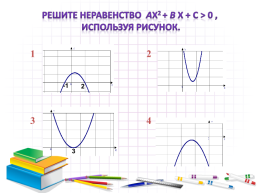
Решите неравенство аx2 + b x + c > 0 , используя рисунок.
1.2
3.4
-1
Слайд 15
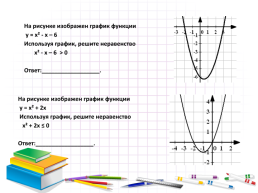
На рисунке изображен график функции
у = х² - х – 6
Используя график, решите неравенство
х² - х – 6 ˃ 0
Ответ:__________________.
На рисунке изображен график функции
у = х² + 2х
Используя график, решите неравенство
х² + 2х ≤ 0
Ответ:__________________.
Слайд 17
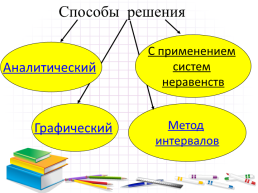
Решение неравенств методом интервалов
x²+x-6=0;
(х+3)(х-2) =0;
Ответ: [-3; 2].
Слайд 18
Работа по учебнику
№ 163 (б)
№ 167 (а)
Работа по карточкам
Слайд 19
Проверка работы по учебнику
Слайд 22
Самостоятельная работа
Вариант 1.
Вариант 2.
№1. Решите неравенства:
а)
а)
б)
б)
№2. Найдите область определения функции:
Желаю удачи!
!
Слайд 23
Проверь своё решение
Вариант 1.
Вариант 2.
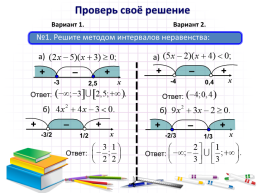
№1. Решите методом интервалов неравенства:
а)
а)
Ответ:
Слайд 24
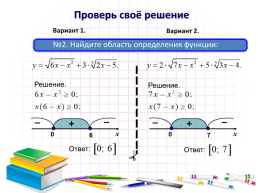
Проверь своё решение
Вариант 1.
Вариант 2.
№2. Найдите область определения функции:
Решение.
Решение.
–
–
–
–
+
+
Слайд 25
Рефлексия урока
Принцип «Микрофон»
На уроке я работал
Своей работой на уроке я Урок для меня показался
За урок я
Мое настроение
Материал урока мне был Домашнее задание мне кажется
активно / пассивно
доволен / не доволен
коротким / длинным
не устал / устал
стало лучше / стало хуже
полезен / бесполезен интересен / скучен легким / трудным интересным / не интересным
Слайд 26
Домашнее задание
На сайте www.mathgia.ru единого банка заданий по ГИА, решить тематический тест “Неравенства”. Подготовиться к проверочной самостоятельной работе работе.
Слайд 27
Спасибо за внимание!
 Организация коррекционно-развивающей работы с детьми с ОВЗ в общеобразовательных учреждениях
Организация коррекционно-развивающей работы с детьми с ОВЗ в общеобразовательных учреждениях Муниципальное бюджетное дошкольное образовательное учреждение «детский сад № 7» г. Усолье – сибирское, иркутская область. Загадки о перелётных птицах. © Субботина татьяна юрьевна воспитатель. 2021 Год
Муниципальное бюджетное дошкольное образовательное учреждение «детский сад № 7» г. Усолье – сибирское, иркутская область. Загадки о перелётных птицах. © Субботина татьяна юрьевна воспитатель. 2021 Год Как оставить отзыв о работе учреждения на официальном сайте для размещения информации о государственных (муниципальных) учреждениях
Как оставить отзыв о работе учреждения на официальном сайте для размещения информации о государственных (муниципальных) учреждениях Межнациональное взаимодействие в Алтайском крае через организацию внеурочной деятельности в общеобразовательных учреждениях
Межнациональное взаимодействие в Алтайском крае через организацию внеурочной деятельности в общеобразовательных учреждениях Методическая деятельность в общеобразовательных учреждениях
Методическая деятельность в общеобразовательных учреждениях Муниципальный смотр методических кабинетов дошкольных образовательных учреждений
Муниципальный смотр методических кабинетов дошкольных образовательных учреждений Социально-экономические методы в организации социальной работы в учреждениях социальной защиты
Социально-экономические методы в организации социальной работы в учреждениях социальной защиты