Презентация - Математика в шахматах

Математика в шахматах
Выполнила: студент группы 20 ПСА 2-9 Попова Олеся Сергеевна Руководитель: учитель математики Савинкова Е.Э.

Цель работы: выявление закономерностей и связей между шахматами и математикой. Объект исследования: шахматы. Предмет исследования: задачи , связанные с шахматными фигурами и шахматной доской.

Отношение шахмат и математики
Подобно тому как математика абстрагируется от конкретности рассматриваемых ею объектов и изучает отношения и формы в чистом виде, так и для шахмат безразлично, из чего сделана доска (в то время как, скажем, для футбола качество травяного покрытия имеет немалое значение), что из себя представляют поля (важно лишь знать, сколько их и какие из них смежны друг с другом) и какого вида шахматные фигуры (существенно лишь, как они ходят). Подобно тому как шахматная партия разворачивается в точном соответствии с правилами игры, не оставляющими сомнения, какой ход возможен, а какой - нет, так и математическая теория развивается на основе своих «правил игры» - аксиом и правил вывода из них; как и шахматный ход, каждый этап математического доказательства должен быть разрешен правилами. Решение шахматной задачи так же неоспоримо, как доказательство математической теоремы: вся шахматная игра целиком укладывается в рамки математики, представляя собой один из видов так называемых исчислений.

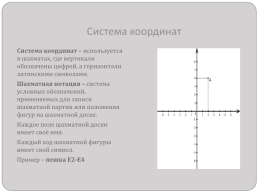
Система координат
Система координат – используется в шахматах, где вертикали обозначены цифрой, а горизонтали латинскими символами. Шахматная нотация – система условных обозначений, применяемых для записи шахматной партии или положения фигур на шахматной доске. Каждое поле шахматной доски имеет своё имя. Каждый ход шахматной фигуры имеет свой символ. Пример – пешка Е2-Е4

Чётность и нечётность в шахматах
На шахматной доске так же есть чётность и нечётность. Тут она связанна с номером хода. При каждом ходе король меняет чётность клеточки на которой он стоит. Например: первый ход - нечётный, второй- чётный и т.д. Одновременно с этим король меняет цвет клетки, на которой он стоит.

Задачи на чётность и нечётность
Задача 1. Конь вышел на поле А1 и через несколько ходов вернулся на него. Докажите, что он сделал чётное число ходов. Вы наверное, заметили, что, делая каждый ход, конь меняет цвет клетки, на которой он стоит. Следовательно: каждый нечётный ход, конь будет вставать на белую клетку. Исходя из этого, конь должен вернуться на клетку А1, чёрного цвета. Мы можем сказать, что он вернётся через чётное число ходов.

Симметрия в шахматах
Разнообразные мотивы симметрии встречаются и на шахматной доске. С одной стороны, речь может идти и о симметрии естественной, то есть возникающей в процессе шахматной партии, а с другой стороны – используемой в шахматных задачах и этюдах. Так же симметрию можно наблюдать в ходах оппонентов. Партии, в которых чёрные повторяют ходы белых, называются обезьяньими.

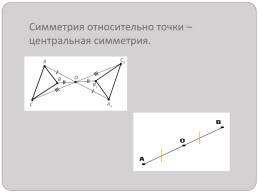
Симметрия относительно точки – центральная симметрия.