Презентация - Разгадав следующий ребус, вы узнаете, каким инструментом можно начертить самую совершенную, по мнению древних греков, плоскую фигуру.. Циркуль

Разгадав следующий ребус, вы узнаете, каким инструментом можно начертить самую совершенную, по мнению древних греков, плоскую фигуру.
ЦИРКУЛЬ

В этом ребусе зашифровано название древнейшего чертёжного инструмента.
ЛИНЕЙКА

Тест: «Взаимное расположение окружностей на плоскости» Условные обозначения: «да» –
«нет» – ___ .

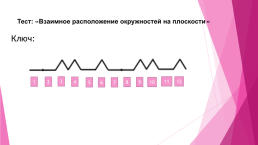
Тест: «Взаимное расположение окружностей на плоскости»
Ключ:

Построение треугольника
Построить треугольник АВС со сторонами 5 см, 3 см и 4 см Цель: Научиться строить треугольник по трем сторонам.

Треугольник – “жесткая” фигура. Если заданы три его стороны, то форму треугольника уже изменить нельзя, не разрушив его. Это свойство широко используется на практике
Делая садовую калитку обязательно прибивают планку/доску/, иногда две планки, чтобы получить треугольники. Это придаёт калитке прочность, иначе её перекосит. 2) Стропила зданий имеют вид треугольников. Это придаёт крепость и устойчивость. 3) При строительстве любых мостов в их конструкциях также присутствуют треугольники. Чем больше треугольников в любой конструкции, тем она прочнее.

В различных конструкциях: Телебашня в Токио

Треугольником называется фигура, которая состоит из трёх точек , не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки.
В
С
А
Точки А, В и С называются вершинами Отрезки АВ, ВС и СА являются сторонами треугольника Обозначение: АВС

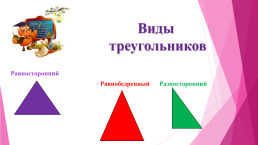
Виды треугольников
Равносторонний Равнобедренный Разносторонний

Построить треугольник АВС со сторонами 5 см, 3 см и 4 см
Строим отрезок АС = 5 см. Строим окружность с центром в точке А и радиусом 3 см. Строим окружность с центром в точке С и радиусом 4 см. Точку пересечения этих окружностей обозначим буквой В – это третья вершина искомого треугольника. Проводим отрезки АВ и ВС. Получили АВС.

Задание Постройте треугольник со сторонами:
1) 3 см, 3 см, 3 см; 2) 4 см, 3 см, 2 см; 3) 5 см, 3 см, 3 см; 4) 6 см, 3 см, 3 см; 5) 8 см, 4 см, 3 см.

Неравенство треугольника
Любая сторона треугольника меньше суммы двух других его сторон

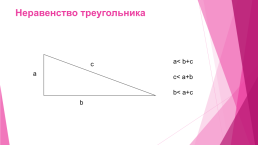
Неравенство треугольника
a< b+c c< a+b b< a+c
c
a
b

Даны три отрезка. Как проверить, можно ли построить треугольник с такими сторонами? Любая сторона треугольника меньше суммы двух других его сторон Или проверить, что наибольший отрезок меньше суммы двух других

Ответы
1 ВАРИАНТ
2 ВАРИАНТ
1. Основание 3,5 см, боковые стороны по 7,5см. 2. Можно построить 3 : 3 см, 4 см, 5 см, т.к. 5 < 3 + 4; 4 см, 5 см, 7 см, т.к. 7 < 4 + 5 ; 3 см, 5 см, 7 см, т.к. 7 < 3 + 5.
1. Основание 4 см, боковые стороны по 8см. 2. Можно построить 2: 2 см, 5 см, 6 см, т.к. 6 < 2 + 5 ; 3 см, 5 см, 6 см, т.к. 6 < 3 + 5 . Нельзя со сторонами 2см, 3см и 5см, т.к. 2 см + 3 см = 5 см

Домашнее задание
По учебнику п. 5.3 № 433, 434 (1б, 2), 439(а) на повторение

Подведение итогов
1. Опишите алгоритм построения треугольника по трем сторонам. 2. Треугольник с любыми ли сторонами можно построить? 3. В чем состоит неравенство треугольника?

Спасибо за работу на уроке!