Презентация - Интегрированный урок по геометрии Оригами и геометрия
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 94%
- Слайдов: 46
- Просмотров: 879
- Скачиваний: 62
- Размер: 48.12 MB
- Класс: 9
- Формат: ppt / pptx
Примеры похожих презентаций
 Интегрированный урок геометрии и технологии в 7 классе «Построение чертежей»
Интегрированный урок геометрии и технологии в 7 классе «Построение чертежей» Интегрированный урок по биологии и химии по теме Чудо фотосинтеза. 10-й класс
Интегрированный урок по биологии и химии по теме Чудо фотосинтеза. 10-й класс Интегрированный урок «Спорт - путь к успеху!»
Интегрированный урок «Спорт - путь к успеху!» Цилиндр. Урок геометрии в 11 классе
Цилиндр. Урок геометрии в 11 классе Интегрированный урок по английскому, немецкому и французскому языкам на тему Достопримечательности Лондона, Парижа и Берлина
Интегрированный урок по английскому, немецкому и французскому языкам на тему Достопримечательности Лондона, Парижа и Берлина Интегрированный урок по физике и музыке в 7 классе «Звуковые явления»
Интегрированный урок по физике и музыке в 7 классе «Звуковые явления» Урок геометрии Удачная окружность
Урок геометрии Удачная окружность
Слайды и текст этой онлайн презентации
Слайд 1

«оригами и геометрия»
Подготовили: учитель математики Пучкина Г.П. и учащиеся 9 классов
Слайд 2

«Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».
Слайд 3

Давно известно, как делаются из бумаги и картона самые различные вещицы: кораблики, самолетики, головные уборы, защищающие голову от солнечных лучей, и оригинальные сувениры из бумаги.
Слайд 4

Оригами – искусство складывания бумаги, пришло из японского языка(«ори» переводится как «сложенный», а кама – «бумага»). Японцы оригами понимают как «искусство целого листа», т. е. изначальное его условие – неразрывность листа бумаги, его целостность без всякого рода вмешательств, прибавлений и других действий по отношению к нему. Только сгибание или складывание листа.
Слайд 5
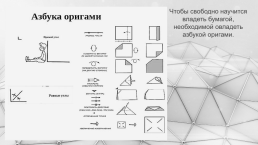
Чтобы свободно научится владеть бумагой, необходимой овладеть азбукой оригами.
Слайд 6
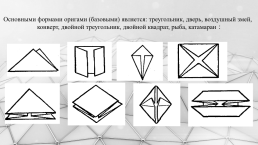
Основными формами оригами (базовыми) является: треугольник, дверь, воздушный змей, конверт, двойной треугольник, двойной квадрат, рыба, катамаран:
Слайд 7

История оригами
Бумага для оригами была изобретена в Китае, а вот первые способы складывания из неё удивительных по красоте фигурок придумали мастера из Японии. В японском языке «Бог» и «бумага» звучат одинаково, «бумага» и «божество» - «ками». В представлениях японцев возникла некая мистическая связь между религиозными ритуалами и изделиями из сложенной бумаги.
Слайд 8

В периоды Камакура (1185 — 1333 гг.) и Муромати (1333 — 1573 гг.) оригами выходит за пределы храмов и достигает императорского двора. Аристократия и придворные должны были обладать определенными навыками и в искусстве складывания. Умение складывать стало одним из признаков хорошего образования и изысканных манер.
В периоды Адзути-Момояна (1573 — 1603 гг.) и Эдо (1603 — 1867 гг.) оригами из церемониального искусства превратилось в популярное времяпрепровождение. Именно тогда, триста-четыреста лет тому назад, изобретается ряд новых фигурок, которые позже становятся классическими. Среди них и японский журавлик (цуру) — традиционный японский символ счастья и долголетия.
Слайд 9

В Стране восходящего солнца существует предание: «Если сложишь тысячу журавликов, то исполнится любое желание, т.к. птица эта обладает бессмертием». Трагическая история японской девочки из Хиросимы, которая после атомной бомбардировки осталась сиротой, обреченной на умирание от лучевой болезни. В больничной палате Садако делала бумажных журавликов, сложила 644 журавлика. До тысячи оставалось еще много…
Слайд 10

Новый этап в развитии оригами начался после второй мировой войны и связан с именем знаменитого японского мастера Акиро Йошизава. Он сыграл в истории оригами уникальную роль. С помощью изобретенных им несложных условных знаков процесс складывания любого изделия оказалось возможным представить в виде серии рисунков-чертежей.
В начале XX века Япония широко открыла двери остальному миру, и европейцы начали знакомиться с классическими фигурками, выполненными в технике оригами: лягушкой, рыбой, журавликом, цветком ириса.
Слайд 11

Слайд 12

Если развернуть фигурку оригами и посмотреть на складки, мы увидим обилие многоугольников, соединенных друг с другом. В сложенном виде оригами представляет собой многогранник, фигуру с множеством плоских поверхностей, а когда фигура разложена и показаны все складки, то называется она двухмерным множеством.
Какую бумагу лучше использовать для оригами?
Слайд 13
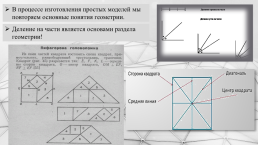
В процессе изготовления простых моделей мы повторяем основные понятия геометрии.
Деление на части является основами раздела геометрии!
Слайд 14
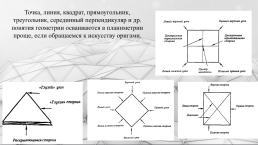
Точка, линия, квадрат, прямоугольник, треугольник, серединный перпендикуляр и др. понятия геометрии осваиваются в планиметрии проще, если обращаемся к искусству оригами.
Слайд 15

С помощью оригами решаются геометрические задачи на плоскости. Выполняя геометрические фигуры в технике оригами, мы знакомимся с новыми геометрическими фигурами в пространстве.
Слайд 16

Модульное оригами - вид объемного оригами. Готовятся одинаковые модули, которые затем вкладываются один в один. Клей не используется.
Слайд 17

Слайд 18

Как вы думаете, сколько модулей?
Слайд 19

Сложное оригами.
Узловое оригами. При создании данных моделей модули соединяются в своеобразные «узлы».
Слайд 20

Кубик оригами
Слайд 21
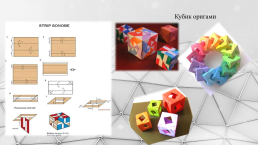
Кубик оригами
Слайд 22

Сонобе шар схема
Слайд 23
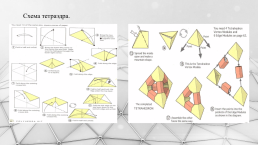
Схема тетраэдра.
Слайд 24

Складывая бумагу в различных комбинациях, создаются модели правильных многогранников с помощью модулей
Куб
Слайд 25

Простое оригами Плоские оригами называют также односторонними оригами: предмет определяется только с одной стороны. Обычно такие изделия используются для аппликации. В этом случае используется клей.
Очень красивыми и эффектными являются аппликации в виде мозаики. Мозаика - это аппликация, элементы которой расположены вплотную друг к другу.
Слайд 26

Слайд 27

ОРИГАМИ – ЭТО ГЕОМЕТРИЯ?
Существует множество сложностей в обучении оригами. Создание оригамной модели требует сосредоточенности и достаточного времени. В начале XIX века немецкий педагог Фридрих Фребель начал пропагандировать складывание из бумаги для объяснения основных правил геометрии.
Все фигуры в оригами выполняются из геометрических фигур, значит это одна из точек прикосновения оригами с математикой. Но в оригами фигуры можно построить без чертежных инструментов, используя несколько сгибов. В конце 20 века возник новый термин «оригаметрия», обозначающий область геометрии, в которой задачи решаются только методом складывания.
Слайд 28

ОРИГАМЕТРИЯ
Слайд 29

Правила (аксиомы) оригаметрии:
Оригаметрия - это сочетание оригами и геометрии, которое несет в себе оригинальность другого подхода к решению задач. В оригаметрии роль прямых играют края листа и линии сгибов, образующиеся при его перегибании; роль точек - вершины углов листа и точки пересечения линий сгибов друг с другом или с краями листов.
Слайд 30
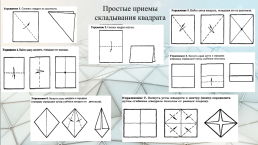
Простые приемы складывания квадрата
Слайд 31
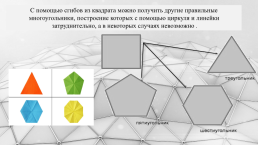
С помощью сгибов из квадрата можно получить другие правильные многоугольники, построение которых с помощью циркуля и линейки затруднительно, а в некоторых случаях невозможно.
Слайд 32
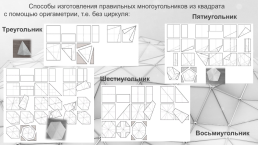
Способы изготовления правильных многоугольников из квадрата с помощью оригаметрии, т.е. без циркуля: Треугольник
Пятиугольник
Шестиугольник
Восьмиугольник
Слайд 33
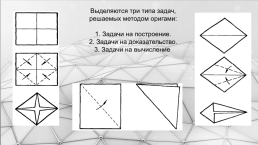
Выделяются три типа задач, решаемых методом оригами: Задачи на построение. Задачи на доказательство. Задачи на вычисление
Слайд 34
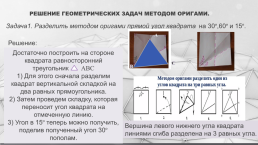
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ МЕТОДОМ ОРИГАМИ.
Задача1. Разделить методом оригами прямой угол квадрата на 30º,60º и 15º.
А
Решение:
Достаточно построить на стороне квадрата равносторонний треугольник АВС 1) Для этого сначала разделим квадрат вертикальной складкой на два равных прямоугольника. 2) Затем проведем складку, которая переносит угол квадрата на отмеченную линию. 3) Угол в 15º теперь можно получить, поделив полученный угол 30º пополам.
С
В
Вершина левого нижнего угла квадрата линиями сгиба разделена на 3 равных угла.
Слайд 35
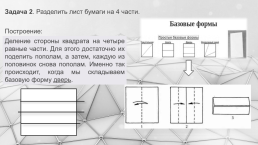
Задача 2. Разделить лист бумаги на 4 части.
Построение:
Деление стороны квадрата на четыре равные части. Для этого достаточно их поделить пополам, а затем, каждую из половинок снова пополам. Именно так происходит, когда мы складываем базовую форму дверь.
Слайд 36
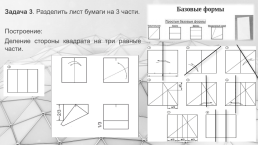
Задача 3. Разделить лист бумаги на 3 части.
Построение:
Деление стороны квадрата на три равные части.
Слайд 37

Задач 4. Разделить лист бумаги на 5 частей.
Построение:
Мы заметили, что особые сложности вызывает деление квадрата на количество частей, являющееся простым числом 3, 5, 7 и т.д. Поэтому деление квадрата на пять частей с помощью складывания представляет собой гораздо более сложную задачу. Ее решение изображено на рисунке.
1) Делаем сгиб, проходящий одновременно через нижний левый угол квадрата и нашу отметку. Правый нижний угол расположен по горизонтали на от верхнего правого края; 2) Делим получившийся отрезок пополам, ширина загнутой полоски и есть ; 3) Расправляем лист и делим на 4 равные части;
4) Складываем левую боковую сторону к намеченной вертикальной складке. Таким образом промежуток делим пополам; 5) Расправляем лист. Широкие полосы осталось поделить пополам
Слайд 38

Задача 5. Доказать методом оригами теорему о сумме углов треугольника.
Доказательство: Возьмем произвольный треугольник; Проведем сгиб через одну из вершин треугольника, перпендикулярно противоположной стороне(высоту); Совместим вершины треугольника с точкой у основания высоты треугольника Получаем, что углы 1, 2 и 3 (составляют в сумме два прямых угла) ABC совпали при наложении с развернутым углом, следовательно, сумма углов треугольника равна 180º.
М
N
Q
R
Слайд 39

Задача 6. Докажем методом оригами теорему о сумме острых углов прямоугольного треугольника =90º.
∠
ВАС и
АСВ
∠
Загнем два острых угла
треугольника АВС так, чтобы их вершины совместились с точкой В. АN = NC. N-середина гипотенузы АС. Со второй линией сгиба тоже-самое. Два острых угла совместились на прямом. Значит сумма двух острых углов равна 90º
Слайд 40

Под рукой оживает бумага, Под рукой оживают цветы, Будто волей искусного мага, Оригами — бумага — мечты...
В технике оригами можно сделать и цветы с использованием схем. Как сделать лилию из бумаги?
Модульное оригами несколько отличается по сложности: для него требуется больше усидчивости и терпения. Однако работы, выполненные в такой технике, выглядят красиво и необычно. Как сделать модульный цветок?
Слайд 41

Проведем сгиб через вершину треугольника.
Задания для самостоятельной работы
1) Возьмите красный треугольник и постройте высоту. Разверните лист бумаги. Все три сгиба прошли через одну точку.
2)Возьмите синий треугольник. Постройте биссектрисы трех углов. Разверните лист бумаги. Внимательно посмотрите на следы сгибов. Все три сгиба прошли через одну точку.
3) Возьмите сиреневый треугольник. Для построения медианы нужно разделить сторону треугольника пополам, для этого совмещаем две вершины треугольника и делаем небольшой сгиб, отмечая тем самым середину стороны. Постройте еще две медианы треугольника.
Слайд 42

Слайд 43

Слайд 44

Слайд 45

Процесс изготовления Оригами очень интересен и увлекателен. Такое занятие развивает эстетический вкус, прививает аккуратность, усидчивость, трудолюбие, творческое отношение к труду, формирует определенные навыки и умения, которые могут пригодиться как в геометрии, так и повседневной жизни.
Слайд 46

Результаты командной работы
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
