Презентация - Урок математики. Решение задач с помощью уравнений урок математики в 5 классе

Урок математики
Решение задач с помощью уравнений урок математики в 5 классе
Автор : Овчинникова Наталья Александровна, учитель математики высшей категории МБУ «Лицей №6» г. Тольятти

Урок математики
Умение решать задачи – такое же практическое искусство, как умение плавать и бегать. Ему можно научиться только путем подражания и упражнения. Д. Пойа

Урок математики
Цели урока:
Знать алгоритм решения уравнений. Уметь решать задачи с помощью уравнений, выделяя три этапа математического моделирования. Развивать умение анализировать, логическое мышление, грамотную математическую речь. Формировать у учащихся положительную мотивацию учения, аккуратность математических записей, умение работать в коллективе.

Урок математики
Разминка: а) Ученик решал уравнение 16 : 2х = 4 так: 16: 2х=4 2х = 16: 4 2х = 4 х = 4: 2 х = 2 Найди ошибку в решении. б) Два ученика решали уравнение 2(х+1)=18 так: 2(х+1)=18 2(х+1)=18 2х+1=18 2х+2=18 2х=18-1 2х=18-2 2х=17 2х=16 х=17: 2 х=16: 2 х=8,5 х=8 Найди верное решение. Объясни свой выбор. Сделай проверку.

Урок математики
Этапы математического моделирования
Составление математической модели
Решение математической модели
Ответ на вопрос задачи

Урок математики
Задача №1
В некотором царстве, в некотором государстве жил-был царь, и было у него у него три сына. Младший в два раза моложе старшего сына и на 9 лет моложе среднего брата. Сколько лет было каждому сыну, если им вместе 85 лет?

Урок математики
Решение:
Пусть младшему сыну было х лет, тогда среднему сыну – (х + 9) лет, а старшему – (2х) лет, по условию задачи вместе им 85 лет, составим уравнение:
Составление математической модели
2х + х + 9 + х = 85 4х + 9 = 85 4х = 85 – 9 4х = 76 х = 76 : 4 х = 19 19 лет – младшему сыну 1) 2· 19 = 38 (лет) – старшему сыну 2) 19 + 9 = 28 (лет) – среднему сыну
Решение математической модели
Ответ на вопрос задачи
Ответ: 38 лет, 28 лет, 19 лет

Урок математики
Задача №2
«И пошли братья счастья пытать, стрелы метать». Стрела старшего брата летела на 25 мин дольше, чем стрела среднего, а стрела младшего летела на 15 мин дольше, чем стрела старшего брата. Сколько минут летела каждая стрела, если общее время полета стрел 125 мин?

Урок математики
Решение:
Пусть стрела среднего сына летела х мин, тогда стрела старшего летела (х + 25) мин, а стрела младшего - (х + 25 + 15) мин, по условию задачи общее время - 125 мин, составим уравнение:
х + 25 + х + х + 25 + 15 = 125 3х + 65 = 125 3х = 125 – 65 3х = 60 х = 60 : 3 х = 20 20 мин – летела стрела среднего 1) 20 + 25 = 45 (мин) – летела стрела старшего 2) 45 + 15 = 60 (мин) – летела стрела младшего
Ответ: 45 мин, 20 мин, 60 мин.

Урок математики
Задача №3
Три снохи царя соткали ковры общей площадью 63 м2. Купеческая дочь соткала ковер в 2 раза больше, чем боярская , а Василиса Премудрая в 2 раза больше купеческой. Сколько квадратных метров ковров соткала каждая девушка?

Урок математики
Решение:
Пусть боярыня соткала ковер площадью х м², Тогда ковер купчихи имел площадь (2х) м² , а ковер Василисы был (2· 2х) м², по условию задачи общая площадь ковров - 63 м², составим уравнение:
х + 2х + 4х = 63 7х = 63 х = 63 : 7 х = 9 9 м² – площадь ковра боярыни 1) 9 · 2 = 18 (м² ) – площадь ковра купчихи 2) 4 · 9 = 36 (м² ) – площадь ковра Василисы
Ответ: 9 м², 18 м², 36 м².

Урок математики
Задача №4
На пиру было выпито 88 л напитков. Трехлитровых чарок медовухи выпито столько же, сколько пятилитровых ковшей кваса. Сколько чарок медовухи было выпито?

Урок математики
Решение:
.Количество ёмкостей (штук).Объём одной ёмкости (л).Общий объём (л)
Чарки.х.3.(3х)
Ковши.х.5.(5х)
88 л
Пусть чарок и ковшей было по х штук, составим уравнение: 3х + 5х = 88 8х = 88 х = 88 : 8 х = 11 11 штук – чарок или ковшей
Ответ: 11 чарок

Урок математики
Задача №5
Чтобы испечь хлеб для царя Василиса Премудрая взяла 10 частей воды, 5 частей муки и 2 части масла (по массе). Сколько граммов каждого вещества надо взять, чтобы приготовить каравай хлеба весом 3 кг 400г?

Урок математики
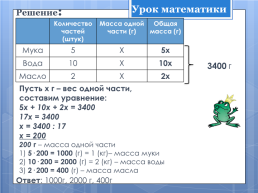
Решение:
.Количество частей (штук).Масса одной части (г).Общая масса (г)
Мука.5.Х.5х
Вода.10.Х.10х
Масло.2.Х.2х
3400 г
Пусть х г – вес одной части, составим уравнение: 5х + 10х + 2х = 3400 17х = 3400 х = 3400 : 17 х = 200 200 г – масса одной части 1) 5· 200 = 1000 (г) = 1 (кг)– масса муки 2) 10· 200 = 2000 (г) = 2 (кг) – масса воды 3) 2· 200 = 400 (г) – масса масла
Ответ: 1000г, 2000 г, 400г

Урок математики
Задача №6
Кощей старше царя на 1037 лет, а царь моложе Кощея в 18 раз. Сколько лет царю и сколько лет Кощею?

Урок математики
Решение:
Пусть Царю было х лет, тогда Кощею было (18х) лет, разница в возрасте составляет (18х – х) лет, по условию задачи – это 1037 лет, составим уравнение:
18х – х = 1037 17х = 1037 х = 1037 : 17 х = 61 61 год – возраст Царя 1) 1037 – 61 = 976 (лет ) – возраст Кощея
Ответ: 61 год, 976 лет.

Урок математики
Итоги урока
Что узнали нового? Чему научились? Что еще хотели бы узнать?
Спасибо за урок!

Урок математики
Список используемых источников
Дорофеев Г. В., Петерсон Л. Г. Математика. 5 класс. – М.: Издательство «Ювента», 2011. Картинки из сказки «Царевна - лягушка» https://www.google.ru/search?q=картинки+из+сказки+царевна+лягушка&newwindow=1&espv=2&biw=1366&bih=635&site=webhp&tbm=isch&tbo=u&source=univ&sa=X&ved=0CBsQsARqFQo