Слайд 1
Домашнее задание
Базовый(задание(я) для всех):
Выучить II признак равенства треугольников.
Уметь отвечать на вопросы 1-4 стр. 55
№ 169, 171, 172
Повышенный(задание(я) по выбору): № 173
Слайд 3
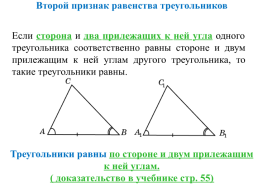
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Треугольники равны по стороне и двум прилежащим к ней углам.
( доказательство в учебнике стр. 55)
Слайд 4
Если сторона и прилежащие к ней углы одного треугольника соответственно равны, стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.
Дано: ∆ ABC, ∆MNK
AB=MN,
Слайд 5
Схема доказательства на II признак равенства треугольников
Рассмотреть два треугольника
Найти пару равных сторон.
Найти первую пару равных углов, прилежащих к этим сторонам
Найти вторую пару равных углов, прилежащих к этим сторонам
Треугольники равны по второму признаку равенства треугольников или по стороне и прилежащим к ним углам
Слайд 6
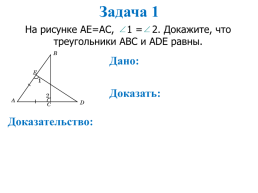
Задача 1
На рисунке AE=AC, 1 = 2. Докажите, что треугольники ABC и ADE равны.
Дано:
Доказать:
Доказательство:
Слайд 7
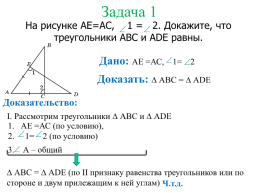
Задача 1
На рисунке AE=AC, 1 = 2. Докажите, что треугольники ABC и ADE равны.
Дано: АЕ =АС, 1= 2
Доказать: ∆ АВС = ∆ ADE
Доказательство:
I. Рассмотрим треугольники ∆ АВС и ∆ АDЕ
АЕ =АС (по условию),
1= 2 (по условию)
3. А – общий
∆ АВС = ∆ АDЕ (по II признаку равенства треугольников или по стороне и двум прилежащим к ней углам)
Ч.т.д.
Слайд 8
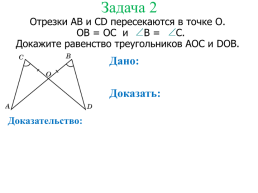
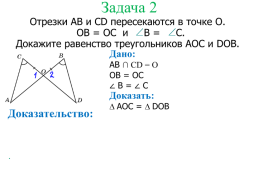
Задача 2
Отрезки АВ и CD пересекаются в точке О.
ОВ = ОС и B = C.
Докажите равенство треугольников АОС и DOB.
Дано:
Доказать:
Доказательство:
Слайд 9
Задача 2
Отрезки АВ и CD пересекаются в точке О.
ОВ = ОС и B = C.
Докажите равенство треугольников АОС и DOB.
Дано:
АВ ∩ CD = О
ОВ = ОС
∠ В = ∠ С
Доказать:
∆ АОС = ∆ DOB
Доказательство:
Слайд 10
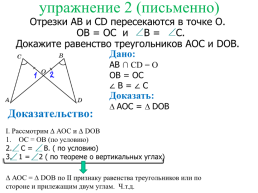
упражнение 2 (письменно)
Отрезки АВ и CD пересекаются в точке О.
ОВ = ОС и B = C.
Докажите равенство треугольников АОС и DOB.
Дано:
АВ ∩ CD = О
ОВ = ОС
∠ В = ∠ С
Доказать:
∆ АОС = ∆ DOB
Доказательство:
I. Рассмотрим ∆ АОС и ∆ DOB
ОС = ОВ (по условию)
С = В. ( по условию)
1 = 2 ( по теореме о вертикальных углах)
∆ АОС = ∆ DOB по II признаку равенства треугольников или по стороне и прилежащим двум углам. Ч.т.д.
Слайд 11
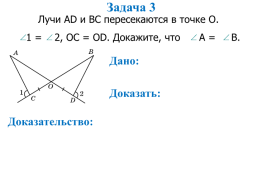
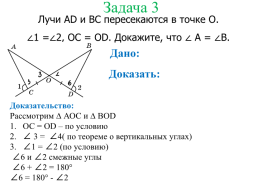
Задача 3
Лучи AD и ВС пересекаются в точке О.
1 = 2, OC = OD. Докажите, что A = B.
Дано:
Доказать:
Доказательство:
Слайд 12
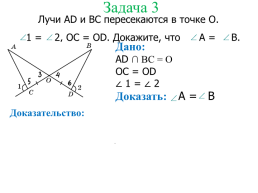
Задача 3
Лучи AD и ВС пересекаются в точке О.
1 = 2, OC = OD. Докажите, что A = B.
Дано:
АD ∩ BC = О
ОC = OD
∠ 1 = ∠ 2
Доказать: A = B
Доказательство:
Слайд 13
Задача 3
Лучи AD и ВС пересекаются в точке О.
∠1 =∠2, OC = OD. Докажите, что ∠ A = ∠B.
Дано:
Доказать:
Доказательство:
Рассмотрим ∆ АОС и ∆ BOD
ОС = ОD – по условию
∠ 3 = ∠4( по теореме о вертикальных углах)
∠1 = ∠2 (по условию)
∠6 и ∠2 смежные углы
∠6 + ∠2 = 180°
∠6 = 180° - ∠2
∠5 и ∠1 – смежные углы
∠5 + ∠ 1 = 180°
∠5 = 180° - ∠1
∠5 = ∠ 6
∆ АОВ = ∆ BOD (ПО II пр)
Слайд 14
Задача 3
Лучи AD и ВС пересекаются в точке О.
∠1 =∠2, OC = OD. Докажите, что ∠ A = ∠B.
Дано:
Доказать:
Доказательство:
Рассмотрим ∆ АОС и ∆ BOD
ОС = ОD – по условию
∠ 3 = ∠4( по теореме о вертикальных углах)
∠1 = ∠2 (по условию)
∠6 и ∠2 смежные углы
∠6 + ∠2 = 180°
∠6 = 180° - ∠2
Слайд 15
В классе (дополнительно) № 168, 170
Домашнее задание
Выучить второй признак равенства треугольников .
Уметь отвечать на вопросы 1-4 стр. 55
Б-№ 169,171,172, п- 173
 Домашнее задание. Базовый(задание(я) для всех): изучить § 8 стр. 52-54 (До второго признака равенства треугольников) вопросы 1–3, № 155, 160, 161 повышенный(задание(я) по выбору): № 163
Домашнее задание. Базовый(задание(я) для всех): изучить § 8 стр. 52-54 (До второго признака равенства треугольников) вопросы 1–3, № 155, 160, 161 повышенный(задание(я) по выбору): № 163 Признаки равенства треугольников
Признаки равенства треугольников Первый признак равенства треугольников - Устный счёт «Задачи на готовых чертежах»
Первый признак равенства треугольников - Устный счёт «Задачи на готовых чертежах» Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников Признаки равенства треугольников
Признаки равенства треугольников Решение задач по теме: «Первый признак равенства треугольников»
Решение задач по теме: «Первый признак равенства треугольников» Задачи на готовых чертежах - Признаки равенства треугольников
Задачи на готовых чертежах - Признаки равенства треугольников