Презентация - Использование таблиц для решения задач

Домашнее задание Решить задачи, составляя таблицы:
1) На первой полке было в 5 раз больше книг, чем во второй. После того, как 12 книг переложили с первой полки на вторую, книг на полках стало поровну. Сколько книг было на каждой полке первоначально? 2) Скорость пешехода меньше скорости велосипедиста на 12 км/ч. Найдите скорость пешехода, если он за 6 часов проходит то же расстояние, какое велосипедист проезжает за 2 часа. 3) За 6 кг мармелада заплатили столько, сколько за 4,8 кг шоколадных конфет. Какова цена каждого вида сладостей, если 1 кг мармелада дешевле 1кг шоколадных конфет на 20р?

17.01.2023
Классная работа
Использование таблиц для решения задач

Основные принципы работы с таблицей
1.Таблица должна быть «живой», действенной моделью, создаваться самим учеником. 2.Принцип единообразия. 3.Таблица должна помогать анализу данных, не обременять решение.

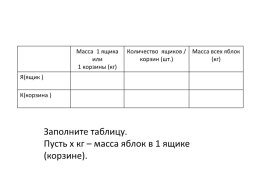
№ 1 В 12 ящиков можно разложить такое же количество яблок, что и в 18 корзин. Определите, сколько килограммов яблок вмещает ящик и сколько корзина, если известно, что в ящик вмещается на 3 кг яблок больше, чем в корзину.

.Масса 1 ящика или 1 корзины (кг).Количество ящиков / корзин (шт.).Масса всех яблок (кг)
Я(ящик )...
К(корзина )...
Заполните таблицу. Пусть х кг – масса яблок в 1 ящике (корзине).

.Масса 1 ящика или 1 корзины (кг).Количество ящиков / Корзин (шт.).Масса всех яблок (кг)
Я(ящик ).x+3.12.12(х+3)
К(корзина ).x.18.18х
ОДИНАКОВО
Т.к. масса яблок в 12 ящиках и 18 корзинах одинаковая, то составим и решим уравнение
12(х+3) = 18х
Масса 1 корзины – 6 кг, 1 ящика – 9 кг

№ 2
Николай рассчитал, что он сможет хорошо приготовиться к экзамену, если будет решать по 12 задач в день. Однако ежедневно он перевыполнял свою норму на 8 задач и уже за 5 дней до экзамена решил на 20 задач больше, чем планировал первоначально. Сколько задач решил Николай?

.Число задач, решенных за 1 д.(з/д).Время (д).Всего задач
Планировал.12.х/12.х
Решил.12+8.(Х+20)/20 на 5 дней меньше.х+20
(Николай, решая за 1 день на 8 задач больше, чем планировал, решил за 5 дней до экзамена на 20 задач больше задуманного), СОСТАВИМ И РЕШИМ УРАВНЕНИЕ
х/12=(х+20)/20 + 5

№ 3
Сколько граммов воды надо добавить к 80 г раствора, содержащего 15% соли, чтобы получить 12%-ный раствор?

.Концентрация соли в растворе.Масса раствора (г).Масса соли в растворе (г)
Было.15% - 0,15.80.0,15*80
Стало.12% - 0,12.80+х.0,12(80+х)
Одинаковая
Т.к. масса соли в растворе остается постоянной, то
СОСТАВИМ И РЕШИМ УРАВНЕНИЕ
0,15*80 = 0,12(80+х)

Задачи на совместную работу
№ 4 Одна бригада может выполнить работу за 6 дней, а другая – за 12 дней. За сколько дней две бригады выполнят ту же работу вместе?

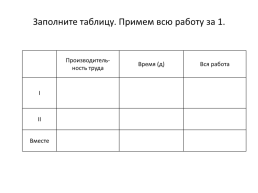
Заполните таблицу. Примем всю работу за 1.
.Производитель- ность труда.Время (д).Вся работа
I...
II...
Вместе...

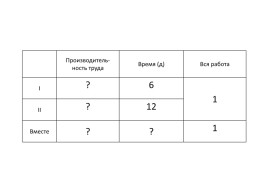
.Производитель- ность труда.Время (д).Вся работа
I.?.6.1
II.?.12
Вместе.?.?.1

Домашнее задание Решить задачи, составляя таблицы:
1)На первой полке было в 5 раз больше книг, чем во второй. После того, как 12 книг переложили с первой полки на вторую, книг на полках стало поровну. Сколько книг было на каждой полке первоначально? Ответ: 6; 30 2) Скорость пешехода меньше скорости велосипедиста на 12 км/ч. Найдите скорость пешехода, если он за 6 часов проходит то же расстояние, какое велосипедист проезжает за 2 часа. Ответ: 6; 18 3) За 6 кг мармелада заплатили столько, сколько за 4,8 кг шоколадных конфет. Какова цена каждого вида сладостей, если 1 кг мармелада дешевле 1кг шоколадных конфет на 20р? Ответ: 80; 100

№ 5 Заказ на пошив сумок был распределен между мастером и его учеником. Мастер выполнил 75% заказа, сшив 90 сумок. Количество сумок, которое шил в день ученик, составило 30% количества сумок, изготовляемых в день мастером, и он работал на 1 день дольше мастера. Сколько сумок в день шил мастер и сколько ученик?

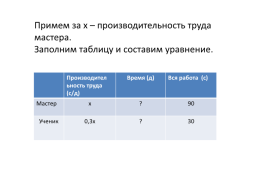
Примем за х – производительность труда мастера. Заполним таблицу и составим уравнение.
.Производител ьность труда (с/д).Время (д).Вся работа (с)
Мастер.х.?.90
Ученик.0,3х.?.30

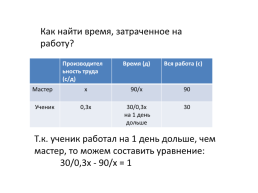
Как найти время, затраченное на работу?
.Производител ьность труда (с/д).Время (д).Вся работа (с)
Мастер.х.90/х.90
Ученик.0,3х.30/0,3х на 1 день дольше.30
Т.к. ученик работал на 1 день дольше, чем мастер, то можем составить уравнение: 30/0,3х - 90/х = 1

Второй способ
Известно, что мастер выполнил 75% заказа, сшив 90 сумок. Каков весь заказ? Сколько сумок сшил ученик? 1)90:0,75=120(с)- весь заказ. 2)120-90=30(с)- сшил ученик.

№ 6 Электротехник и его ученик вместе выполнили работу за 8 часов. За сколько часов эту работу мог бы выполнить электротехник, работая один, если известно, что его ученик работает в 2 раза медленнее?

Пусть электротехник может выполнить эту работу за х ч. Тогда ученик за 2х ч. Заполните таблицу и составьте уравнение.
.Производительность труда.Время (ч).Вся работа
Электротехник.1/х.х.1
Ученик.1/2х.2х.
Вместе.1/х + 1/2х.8.1
Т.к. за 8 ч, работая вместе, они выполнили всю работу, то 8(1/х+1/2х) = 1