Презентация - Решение задач на смеси для 9 класса

Решение задач на смеси
Учитель математики МБОУСОШ №1 г. Южи Ивановской области Чурина Елена Вениаминовна

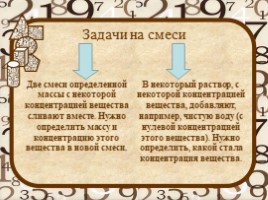
Задачи на смеси
Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.

Алгоритм решения задач на смеси 
1.Определить, какое вещество влияет на концентрацию раствора (главное вещество). 2.Следить за весом главного вещества при добавлении других веществ в раствор. 3. Исходя из данных об изменениях состояния главного вещества - сделать выводы.

Задача №1
В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Объем вещества в растворе Концентрация вещества Объем раствора
1-й раствор
2-й раствор
Смесь
5∙0,12=0,6л
12%=0,12
5л
0
0
7л
0,6+0=0,6л
х%
12л
В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Исходя из определения концентрации, составим пропорцию:
0,6 : 12 = х : 100
х = (0,6 ∙ 100) : 12
х = 5
Ответ: 5%

Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Задача №2

Объем вещества в растворе Концентрация вещества Объем раствора
1-й раствор
2-й раствор
Смесь
Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
4∙0,15=0,6л
15%=0,15
4л
6∙0,25=1,5 л
25%=0,25
6л
0,6+1,5=2,1л
х%
10л

Исходя из определения концентрации, составим пропорцию:
2,1 : 10 = х : 100
х = 2,1 ∙ 100 : 10
х = 21
Ответ: 21%

1. Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? 2. Сколько миллилитров 55% раствора уксуса нужно добавить к 500 миллилитрам 1% раствора, чтобы получить 5% раствор уксуса?
Задачи для самостоятельного решения

Список использованных источников
1.Статья «Задачи на смеси и сплавы. Начальный уровень» https://youclever.org/book/zadachi-na-smesi-i-splavy-1 2. .Статья «Метод Пирсона в решении задач на сплавы и смеси» Источник шаблона Шумарина Вера Алексеевна, учитель математики ГКС(К)ОУ С(К)ОШ №11 VIII вида г.Балашова Саратовской области