Презентация - Использование графов при решении задач (11.04.2019)

Использование графов при решении задач
9 класс
Автор: Александрова З.В., учитель физики и информатики, МБОУ СОШ №5 пгт Печенга, Мурманская область
2018 г.

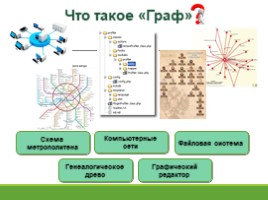
Что такое «Граф»
Схема метрополитена
Генеалогическое древо
Компьютерные сети
Файловая система
Графический редактор

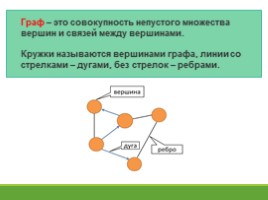
Граф – это совокупность непустого множества вершин и связей между вершинами. Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.

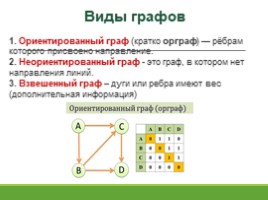
Виды графов 1. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление. 2. Неориентированный граф - это граф, в котором нет направления линий. 3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация)

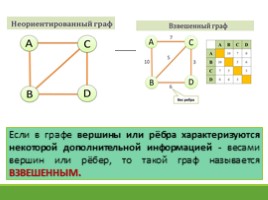
Если в графе вершины или рёбра характеризуются некоторой дополнительной информацией - весами вершин или рёбер, то такой граф называется ВЗВЕШЕННЫМ.

Два варианта значения слова «граф» 1) удобная форма описания структур типа дорожной сети или сети передачи данных; 2) математический объект G := (V, E), где V — это непустое множество вершин, E — множество ребер (пар вершин).

Для описания графа часто используют квадратную таблицу, которая описывает все возможные связи между узлами (без учета дублирования) – матрицу.
А Б В Г
А 5 8
Б 5 11 3
В 11 7
Г 8 3 7
ВЕСОВАЯ МАТРИЦА

Задача 1.

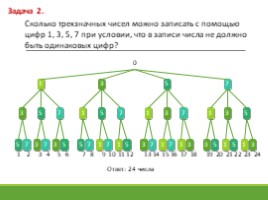
Сколько трехзначных чисел можно записать с помощью цифр 1, 3, 5, 7 при условии, что в записи числа не должно быть одинаковых цифр?
0
1
3
5
7
3
5
7
1
3
5
1
5
7
1
3
7
5
7
3
7
3
5
5
7
1
7
1
5
3
7
1
7
1
3
3
5
1
5
1
3
Ответ: 24 числа
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Задача 2.

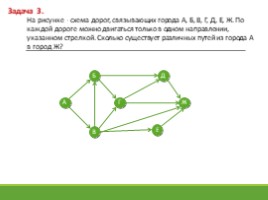
На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
А
Б
В
Г
Д
Ж
Е
1. А-Б-Д-Ж
2. А-Б-Г-Д-Ж
3. А-Б-Г-Ж
4. А-В-Б-Д-Ж
5. А-В-Б-Г-Д-Ж
6. А-В-Б-Г-Ж
7. А-В-Г-Д-Ж
8. А-В-Г-Ж
9. А-В-Ж
10. А-В-Е-Ж
Ответ: 10 путей
Задача 3.

Задача 4.

Задача 3.
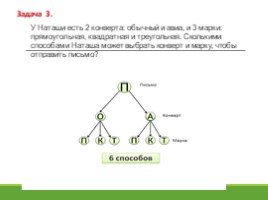
У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?

Задача 5.
Решение: Обозначим ученых вершинами графа и проведем от каждой вершины линии к четырем другим вершинам. Получаем 10 линий, которые и будут считаться рукопожатиями.

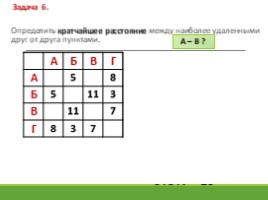
Определить кратчайшее расстояние между наиболее удаленными друг от друга пунктами.
А Б В Г
А 5 8
Б 5 11 3
В 11 7
Г 8 3 7
А – В ?
А
Г
Б
5
8
В
Г
11
3
В
7
5+3+7 = 15
Задача 6.

1. Определение вершины. 2. Построение графа.
3. Ответ ABDEF=12
E,2
Задача 7.

Задача 8.

Задача 9.
(Самостоятельно)

Задача 10.
(Самостоятельно)

Спасибо за работу на уроке!