Презентация - Основное свойство дроби

Основное свойство дроби

Вспомним!
Из данных чисел выбирете обыкновенные дроби: 3,7 ; ; ; 0,1 ; ; 0; 8,0089; ; .
Прочитайте их, что показывают знаменатель и числитель каждой дроби? Что в этой записи означает дробная черта?

Какая часть фигуры закрашена?

Ответьте на вопросы
1. Какую часть часа составляет 1 минута? 2. Какую часть урока составляют 13 минут? 3. Какую часть метра составляет 1 см?

Задача №1
Коля на день рождения пригласил четырех друзей. Мама испекла торт и разделила его на пять равных частей. Но гости решили, что кусочки слишком большие, и попросили разрезать каждый кусок еще на две части. Торт оказался таким вкусным, что каждый из них съел по два куска. Какую часть торта съел каждый и какую часть должен был получить сначала? Сравните полученные доли. Запишите результат с помощью дробей.
=

Задача №2
Начертите квадрат со стороной 8 клеток. Разделите его на два равных прямоугольника. Закрасьте один из них. Запишите, какая часть квадрата закрашена. Этот же квадрат разделите на 4 равных квадрата. Запишите, какая часть квадрата закрашена. Этот же квадрат разделите на 8 равных прямоугольников. Запишите, какая часть квадрата закрашена. Проанализируйте полученный результат и сделайте записи.
=
=

Задача №3
Опираясь на результаты первых двух задач, выполните задание: подберите дроби равные .
?
=

Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Основное свойство дроби
Основное свойство дроби
=
b  m
b
=
b
b : m

Умножьте числитель и знаменатель дроби на 3 и запишите полученные равенства:

Из каких частей состоит обыкновенная дробь?
Числитель Дробная черта Знаменатель

Какая дробь называется правильной?
Дробь называется правильной, если ее числитель меньше знаменателя. Т.е. a < b

Какая дробь называется неправильной?
Дробь называется неправильной, если ее числитель больше знаменателя или равен ему. Т.е. a > b или a = b

Распределите по столбикам дроби:
Правильные дроби.Неправильные дроби
.

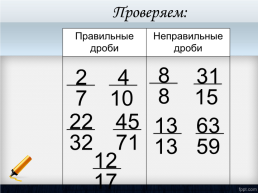
Проверяем:
Правильные дроби.Неправильные дроби
.

Как изменится дробь, если увеличить её числитель в несколько раз?
Вывод: Если Числитель дроби увеличить в несколько раз, не изменяя знаменателя, то дробь увеличится во столько же раз.

Как изменится дробь, если уменьшили числитель в несколько раз?
Вывод: Если числитель дроби уменьшить в несколько раз, не изменяя знаменателя, то дробь уменьшится во столько же раз.

Как изменится величина дроби при увеличении её знаменателя в несколько раз?
Вывод: Если знаменатель дроби увеличить в несколько раз, не изменяя числителя, то и дробь уменьшится во столько же раз.
=
=
=
=

Как изменится величина дроби при уменьшении её знаменателя в несколько раз?
Вывод: Если знаменатель дроби уменьшить в несколько раз, не изменяя числителя, то и дробь увеличится во столько же раз.

А что произойдёт с величиной дроби при одновременном увеличении или уменьшении числителя и знаменателя в одно и то же число раз ?
.
???
Если числитель и знаменатель дроби увеличить в одинаковое число раз, то дробь не изменится.
Если числитель и знаменатель Дроби уменьшить в одинаковое Число раз, то дробь не изменится.

Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
а в
аn вп
а:m в:m
а в
.,
=
=

Сокращать, сократить что-то – укоротить, уменьшить. Толковый словарь живого великорусского языка В.И.Даля

Сократить дробь
=
=

Сокращение дробей.
Дана дробь:
На какие числа можно разделить и числитель и знаменатель?

Сокращение дробей.
Такое преобразование называют сокращением дробей.
Разделим и числитель и знаменатель дроби на 12.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
Равные дроби

1 способ сокращения дробей.
Сокращать дроби можно постепенно, используя признаки делимости чисел.

2 способ сокращения дробей.
Сокращать дроби можно используя нахождение НОД.
НОД(135; 180) = 45

3 способ сокращения дробей.
Сокращать дроби можно используя разложение чисел на множители.
275
935
1810
9225
22

ОПРЕДЕЛЕНИЕ:
Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой. Дробь сокращают до тех пор, пока в числителе и знаменателе не получат взаимно простые числа.

Назовите дроби, которые невозможно сократить:

Несократимая дробь

Закрепление.
Назвать несократимые дроби:

1.Выпишите несократимые дроби:

ИТОГ УРОКА.
2. Какую часть составляет:
а) 20 от 70; б) 12 от 60; в) 14 от 49?

Сократите дробь:
Нарисуйте получившуюся дробь у себя в тетради.