Презентация - Методы решения задач с экономическим содержанием

Методы решения задач с экономическим содержанием
Айдаркина Любовь Семёновна, учитель первой категории, МБОУ «СОШ №2», п.Пурпе

Актуальность выбранной темы
Данная тема актуальна с точки зрения освоения материала для практического применения знаний не только в математике, но в реальных жизненных ситуациях, в частности, применение ее в экономической сфере

Цель работы:
Показать один из методов решения задачи №19 из сборника задач ЕГЭ по математике

Задачи с экономическим содержанием являются практическими задачами. А их решение, бесспорно, способствует более качественному усвоению содержания курса математики средней школы, позволяет осуществлять перенос полученных знаний и умений в экономику, что в свою очередь, активизирует интерес школьников к задачам прикладного характера и изучению математики в целом. Такие задачи позволяют наиболее полно реализовывать прикладную направленность в обучении и способствуют более качественному усвоению самого учебного материала и формированию умения решать задачи данного типа.

1% числа а – это Р % числа - это Увеличение числа а на р% Уменьшение числа а на р%

Задача 1
31 декабря 2016 года Сергей взял в банке 9930000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся часть долга ( то есть увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какова должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами.

Решение:
Пусть сумма кредита S млн.рублей, кредит взят под а% годовых на 3 года, тогда за этот срок , оставшаяся сумма долга умножается на коэффициент к=1+0,01а, S=9930000р. Х руб.- ежегодные выплаты, тогда, а=10% Sк (Sк-х)к ((Sк-х)к-х)к Х Х Х S (Sк-х) (Sк-х)к-х ((Sк-х)к-х)к-х=0 ((Sк-х)к-х)к-х=0, (Sк2-кх-х)к-х=0, Sк3- к2х-кх-х=0, Sк3= к2х+кх+х, х=3993000 (руб.) Ответ:3993000 рублей

Задача 2
31 декабря 2016 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся часть долга ( то есть увеличивает долг на 10%), затем Михаил переводит в банк 2928200 рублей . Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за 4 года).

Решение
Sмлн.руб-сумма кредита, а=10%, х = 2928200 рублей Sк (Sк-х)к ((Sк-х)к-х)к ((Sк-х)к-х)к-х Х Х Х Х S (Sк-х) (Sк-х)к-х ((Sк-х)к-х)к-х (((Sк-х)к-х)к-х)к-х=0 (((Sк-х)к-х)к-х)к-х=0, S=9282000(руб.) Ответ: 9282000 рублей взял в банке.

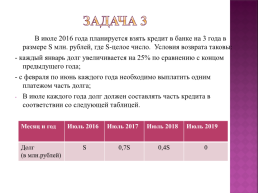
Задача 3
В июле 2016 года планируется взять кредит в банке на 3 года в размере S млн. рублей, где S-целое число. Условия возврата таковы: - каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; В июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Месяц и год.Июль 2016.Июль 2017.Июль 2018.Июль 2019
Долг (в млн.рублей).S.0,7S.0,4S.0

Найдите наибольшее значение S, при котором каждая из выплат будет меньше 3 млн. рублей. Решение: Пусть S-сумма кредита, а=25%, а тогда Х1, Х2, Х3 – платежи, к=1,25 1) Sк- Х1=0,7 S в июле 2017г 2) 0,7Sк- Х2=0,4 S – 2018г 3) 0,4 Sк-Х3=0, Х3=0,4∙1,25 S, Х3=0,5 S, 4) Х2=0,475 S, 5) Х1=0,55 S. Самая большая выплата Х1=0,55 S. 0,55 S<3, S=5 Ответ: 5млн.рублей

3адача 4
По бизнес-плану четырехлетний проект предполагает начальное вложение – 10 млн. рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн.рублей, и в первый, и во второй годы, а также целое число m млн. рублей и в третий, и в четвертый год. Найдите наименьшее значение n, при котором первоначальные вложения за два как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значение n первоначальные вложения за четыре года как минимум утроятся

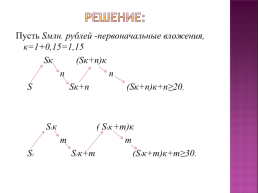
Решение:
Пусть Sмлн. рублей -первоначальные вложения, к=1+0,15=1,15 Sк (Sк+n)к n n S Sк+n (Sк+n)к+n≥20. S1к ( S1к +m)к m m S1 S1к+m (S1к+m)к+m≥30.

К началу 2-го года получится 1,15 ·10 + n = 1 1,5 + n (млн) вложений, а к началу 3-го года — 1,15(11,5 + n) + n =13,225 + 2,15n . По условию 13,225 + 2,15n ≥ 20 . Наименьшее целое решение n = 4. Тогда к началу 3-го года получится S1=13,225 + 8,6 = 21,825 млн. К началу 4-го года имеем 1,15 ∙ 21,825 + m (млн), а в конце проекта 1,15(1,15∙ 21,825+m) +m=1,3225·21,825+ 2,15m= 28,86 + 2,15m. По условию 28,86 + 2,15m ≥ 30 . Получаем, что m =1 – наименьшее целое решение. Ответ: 4 и 1 млн руб.