Презентация - Фракталы

ФРАКТАЛЫ
В КОМПЬЮТЕРНОЙ ГРАФИКЕ

"Многие вещи нам непонятны не потому, что наши понятия слабы, а потому, что сии вещи не входят в круг наших понятий» Козьма Прутков
Фракталы - самые красивые, очаровательные и странные порождения геометрии XX века. Это детища сухой математики, но они настолько эстетичны, что выставка фракталов, построенных с помощью компьютера потрясла мир, а книга организаторов выставки Хайнца-Отто Пайтгена и Петера Рихтера, "Красота фракталов" раскупалась как художественный альбом. Они упорядочены, но это не упорядоченность монотонного орнамента, повторяющего без изменений один и тот же мотив. Они геометричны, но это геометрия не идеалиста Платона, искавшего везде отполированные формы правильных многогранников, а геометрия реального мира - ветвистого, пористого, шершавого, зазубренного, изъеденного. Не зря человек, давший фракталам имя, - польский математик Мандельброт с французским именем Бенуа, проработавший большую часть жизни на американскую корпорацию IBM, - назвал свой главный труд "Фрактальная геометрия природы".

" Облака не сферы, горы - не конусы, линии берегов - не окружности, и не гладка древесная кора и не прям путь молнии» Бенуа Мандельброт, Фрактальная геометрия природы, 1982
Основное свойство фракталов - самоподобие. Любой микроскопический фрагмент фрактала в том или ином отношении воспроизводит его глобальную структуру. В простейшем случае часть фрактала представляет собой просто уменьшенный целый фрактал. Отсюда основной рецепт построения фракталов: возьми простой мотив и повторяй его, постоянно уменьшая размеры. В конце концов выйдет структура, воспроизводящая этот мотив во всех масштабах, - бесконечная лестница вглубь. Как форма и размер отдельных элементов, так и их взаимное расположение может быть описано математической формулой.

Фрактальная графика может применяться во многих областях естественных наук. Фракталы помогают геофизикам определять и предсказывать форму и характер растрескиваний земной коры и особенности распределения в ее слоях различных химических элементов, а астрономам – моделировать формирование планетных систем и галактик, характер рассеивания лучей и космической пыли. Многие природные объекты также самоподобны и состоят из повторяющихся элементов разных размеров. Очевидные примеры – дерево, куст, колония кораллов.
Еще более наглядным примером может служить соцветие «сложный зонтик» – «зонтик», состоящий, в свою очередь, из маленьких зонтиков. На рисунке слева показано соцветие растения из семейства зонтичных, а справа - его схема, построенная с использованием фрактальной графики.

Фрактальная графика
Фрактальная графика, как и векторная — вычисляемая, но отличается от нее тем, что никакие объекты в памяти компьютера не хранятся. Фрактальное изображение строится по уравнению (или по системе уравнений), поэтому ничего, кроме формулы, хранить не надо. Изменив коэффициенты в уравнении, можно получить совершенно другую фрактальную картину. Для выполнения расчетов, связанных с фрактальной геометрией, и графического представления получающихся результатов существует множество различных компьютерных программ. В их основе лежит возможность ввода базовой формулы, отражающей предполагаемый тип элемента фрактала и ее последующих изменений, позволяющих трансформировать фигуры – элементы фрактала: увеличивать их или уменьшать, поворачивать относительно центра рисунка или начальной точки и, главное, задавать количество вложений, т.е. число шагов программы.

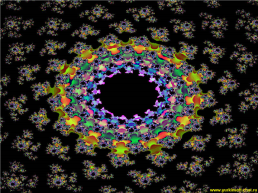
Построение фракталов
Простейшим фрактальным объектом является фрактальный треугольник. 1. Постройте обычный равносторонний треугольник. 2. Разделите каждую из его сторон на три отрезка.
3. На среднем отрезке стороны постройте равносторонний треугольник со стороной, равной 1/3 стороны исходного треугольника, а на других отрезках постройте равносторонние треугольники со стороной, равной 1/9. 4. С полученными треугольниками повторите те же операции. Вскоре вы увидите, что треугольники последующих поколений наследуют свойства своих родительских фрактальных структур. 5. Так рождается фрактальная фигура.

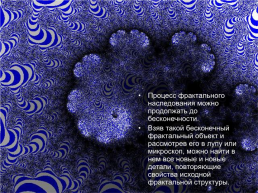
Процесс фрактального наследования можно продолжать до бесконечности. Взяв такой бесконечный фрактальный объект и рассмотрев его в лупу или микроскоп, можно найти в нем все новые и новые детали, повторяющие свойства исходной фрактальной структуры.

Построение фракталов
Еще один известный фрактал – кривая Коха. Берем отрезок и среднюю его треть переламываем под углом 60 градусов. Затем повторяем эту операцию с каждой из частей получившейся ломаной - и так до бесконечности. В результате мы получим простейший фрактал - триадную кривую, которую в 1904 году открыла математик Хельга фон Кох. Если на каждом шаге не только уменьшать основной мотив, но также смещать и поворачивать его, можно получить более интересные и реалистически выглядящие образования, например, лист папоротника или даже целые их заросли.

Построение фракталов
Фрактальными свойствами обладают многие объекты живой и неживой природы. Обычная снежинка, многократно увеличенная, оказывается фрактальным объектом. Фрактальные алгоритмы лежат в основе роста кристаллов и растений. Взгляните на ветку папоротникового растения, и вы увидите, что каждая дочерняя ветка во многом повторяет свойства ветки более высокого фрактального уровня. В отдельных ветках деревьев чисто математическими методами можно проследить фрактальные свойства всего дерева. А если ветку поставить в воду, то вскоре можно получить саженец, который со временем разовьется в полноценное дерево (это легко удается сделать с веткой тополя).

Известные фракталы
Фрактал Серпинского (на плоскости)
Решетка Серпинского  и Губка Серпинского  (объемные фракталы)

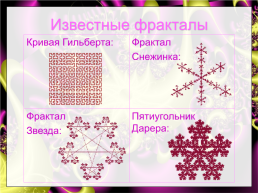
Известные фракталы
Кривая Гильберта:.Фрактал Снежинка:
Фрактал Звезда:.Пятиугольник Дарера:

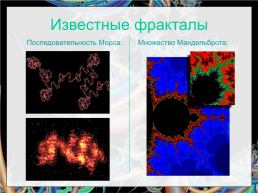
Известные фракталы
Последовательность Морса:.Множество Мандельброта:
.

Известные фракталы
Множество Жюлиа:.
.

Фрактальная графика
Можно построить весьма правдоподобный фрактальный рельеф местности и покрыть её очень симпатичным лесом.
Большинство текстур местности в современных компьютерных играх представляют фракталы.

Как только Мандельброт открыл понятие фрактала, оказалось, что мы буквально окружены ими. Фрактальны слитки металла и горные породы, фрактальны расположение ветвей, узоры листьев, капиллярная система растений; кровеносная, нервная, лимфатическая системы в организмах животных, фрактальны речные бассейны, поверхность облаков, линии морских побережий, горный рельеф...
В 3D Studio Max, например, для генерации деревьев используется фрактальный алгоритм.