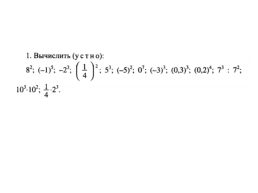Презентация - Корень n-ой степени и его свойства

Корень n-ой степени и его свойства

Определение:
Корнем n-ной степени из числа a называется такое число, n-ная степень которого равна a.

Число корней данного уравнения зависит от n и a.

Арифметический корень n-ой степени
Арифметическим корнем n-й степени из числа а называют неотрицательное число, n-я степень которого равна a.

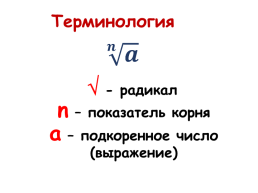
Терминология
 - радикал n – показатель корня a – подкоренное число (выражение)

Примеры:

Рассмотрим примеры:
1) Решите уравнение:

Рассмотрим примеры:
2) Решите уравнение:

Таким образом, делаем вывод:
При n-чётном существуют два корня n-й степени из любого положительного числа a; корень n-й степени из числа 0 равен нулю; корней чётной степени из отрицательных чисел не существует.

При нечётном n существует корень n-й степени из любого числа a, и притом только один!

Основные свойства корней:

Теорема 1. Корень n-ой степени (n = 2, 3, 4, …) из произведения двух неотрицательных чисел равен произведению корней n-ой степени из этих чисел.
Пример 2. Вычислить:
Пример 1. Вычислить:

Теорема 2. Корень n-ой степени из отношения неотрицательного числа a и положительного числа b равен отношению корней n-ой степени из этих чисел.
Пример 3. Вычислить:
Пример 4. Вычислить:

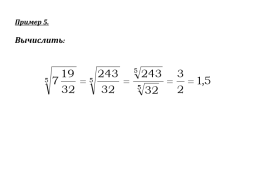
Пример 5. Вычислить:

Теорема 3. Чтобы возвести корень n-ой степени из неотрицательного числа a в натуральную степень k, надо в эту степень возвести подкоренное выражение.
Пример 6. Вычислить:

Теорема 4. Чтобы извлечь корень n-ой степени из корня k-ой степени из неотрицательного числа a, надо извлечь корень kn-ой степени из этого числа.
Пример 7. Упростить выражение:

Теорема 5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же число, то значение корня не изменится.
Пример 8.
Пример 9. Упростим выражение:

Теорема 6. Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное выражение и из результата извлечь тот же корень

Пусть a>0, тогда

Самостоятельная работа
Вариант 1.
Вариант 2.
1. Вычислите:
2. Упростите выражение:

Самопроверка самостоятельной работы.
Вариант 1.
Вариант 2.
1. Вычислите:
2. Упростите выражение:

Домашнее задание!!!

Домашняя работа
Вычислить 2. Вычислить 3. Вычислить а) б) Упростить: а) б) в) 5. Выполнить действия: