Презентация - Магические квадраты

«Магические квадраты»
Автор: учитель математики Сидорова М.В.

Высшее назначение математики…состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает. Н.Винер
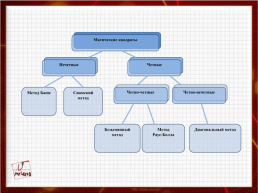
Цель : изучить некоторые способы заполнения магических квадратов (Баше, Раус-Болла, Сиамский (А.де ла Лубера), диагональный)

Задачи:
ознакомиться с историей появления магических квадратов; выяснить виды магических квадратов; ознакомиться с различными методами заполнения магических квадратов.

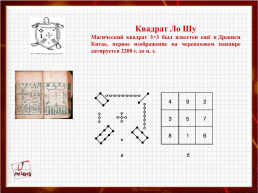
Квадрат Ло Шу Магический квадрат 3×3 был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 г. до н. э.

В древнеиндийских надписях и трактатах встречаются изображения магических квадратов четвертого порядка.
1.14.15.4..7.12.1.14
12.7.6.9..2.13.8.11
8.11.10.5..16.3.10.5
13.2.3.16..9.6.15.4

Немецкий художник Альбрехт Дюрер (1471-1528), выпустивший в 1514 году гравюру «Меланхолия», на которой в правом верхнем углу есть изображение магического квадрата четвертого порядка. Причем два числа в середине нижней строки указывают на год создания гравюры - 1514.

Известный немецкий гуманист Корнелий Генрих Агриппа (1486-1535) построил магические квадраты порядков 3, 4, 5, 6, 7, 8, 9 — он связал их с семью астрологическими «планетами» — Сатурном, Юпитером, Марсом, Солнцем, Венерой, Меркурием, и Луной.
В 1654 году французский ученый Блез Паскаль написал трактат, полностью посвященный магическим квадратам.

Метод Баше
Квадрат дополняется вспомогательными клетками с четырех сторон «лесенкой» или «террасами» как показано на рисунке. Последовательные числа от 1 до n выписываются ряд за рядом в направлении, параллельном одной из диагоналей квадрата. Числа, оказавшиеся за рамками квадрата, нужно ввести внутрь. Для этого «террасы» мысленно вдвигаем в квадрат так, чтобы они примкнули к противолежащим сторонам квадрата.

Сиамский метод (А.де ла Лубера)
Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата, продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца (по ломаной диагонали). Дойдя до правого края квадрата, продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки или угла, траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.

Метод Раус-Болла
Метод Раус-Болла начинается с того, что квадрат заполняется слева направо и сверху вниз числами от 1 до n2 в их естественном порядке. Затем выполняются перестановки чисел в некоторых клетках, после чего квадрат становится магическим.

Диагональный метод
Рассмотрим случай, когда после деления квадрата на четыре равные части, каждая из них становится квадратом нечетного порядка. Построение четно-нечетного магического квадрата производится аналогично построению четно-четного квадрата, но в этом случае применяется три типа перестановок чисел в клетках.

Выводы:
Универсального способа заполнения магических квадратов нет. Способ заполнения магического квадрата, зависит от его порядка. Известные методы для заполнения магических квадратов можно автоматизировать. Для этого идеально подходит программа MS Excel.