Презентация - Применение аксиом и их следствий

1
Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори, Мурманской обл.
Применение аксиом
и их следствий
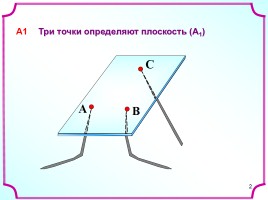
Геометрия 10

2

3
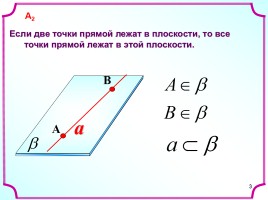
a
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
A
B
А2

4
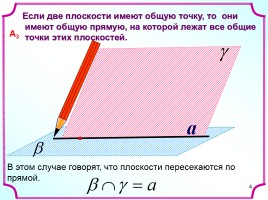
a
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
А3

5
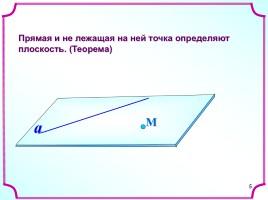
Прямая и не лежащая на ней точка определяют плоскость. (Теорема)
М
a

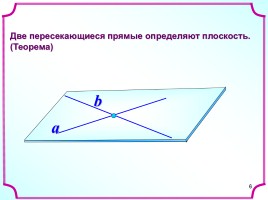
6
Две пересекающиеся прямые определяют плоскость. (Теорема)
a
b

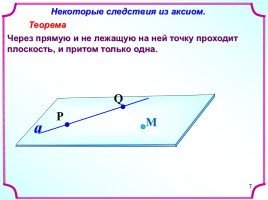
7
Некоторые следствия из аксиом.
Теорема
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
М
a

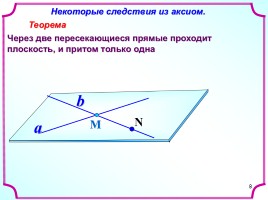
8
Некоторые следствия из аксиом.
Теорема
Через две пересекающиеся прямые проходит плоскость, и притом только одна
М
a
b
N

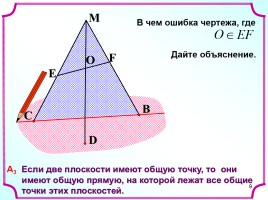
9
С
Е
М
О
F
B
D
А3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В чем ошибка чертежа, где Дайте объяснение.

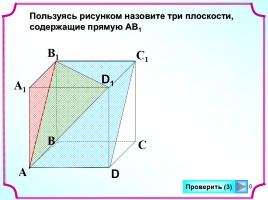
10
А
В
С
D
А1
В1
С1
D1
Пользуясь рисунком назовите три плоскости, содержащие прямую АВ1
Проверить (3)

11
Проверить (2)
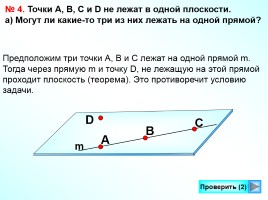
№ 4. Точки А, В, С и D не лежат в одной плоскости. а) Могут ли какие-то три из них лежать на одной прямой?
Предположим три точки А, В и С лежат на одной прямой m. Тогда через прямую m и точку D, не лежащую на этой прямой проходит плоскость (теорема). Это противоречит условию задачи.
m

12
Проверить (2)
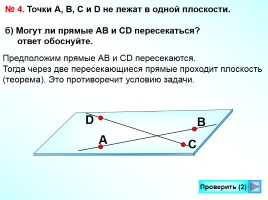
№ 4. Точки А, В, С и D не лежат в одной плоскости. б) Могут ли прямые АВ и СD пересекаться? ответ обоснуйте.
Предположим прямые АВ и СD пересекаются. Тогда через две пересекающиеся прямые проходит плоскость (теорема). Это противоречит условию задачи.

13
Проверить
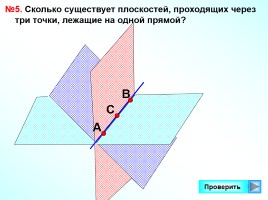
№5. Сколько существует плоскостей, проходящих через три точки, лежащие на одной прямой?
А
С
В

14
Проверить (2)
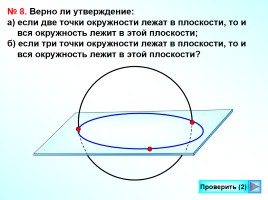
№ 8. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?

15
Проверить (3)
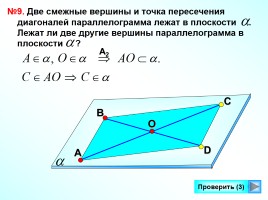
№9. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли две другие вершины параллелограмма в плоскости ?
С
А
В
D
O

16
Проверить (2)
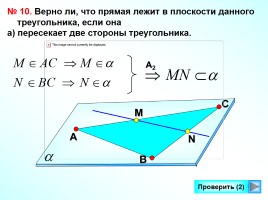
№ 10. Верно ли, что прямая лежит в плоскости данного треугольника, если она а) пересекает две стороны треугольника.
С
А
В

17
Проверить (2)
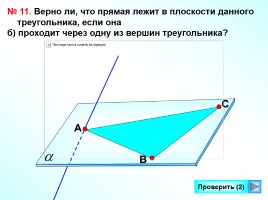
№ 11. Верно ли, что прямая лежит в плоскости данного треугольника, если она б) проходит через одну из вершин треугольника?
С
А
В

18
Проверить (3)
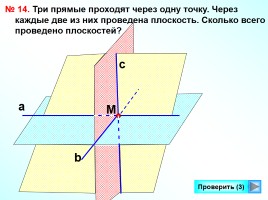
№ 14. Три прямые проходят через одну точку. Через каждые две из них проведена плоскость. Сколько всего проведено плоскостей?
М
а
b
c