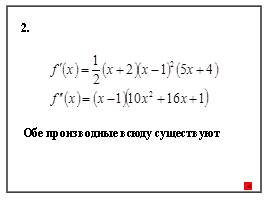Презентация - Исследование функции и построение ее графика

Исследование функции и построение ее графика

В данной работе будем исследовать функцию

Общая схема исследования функции
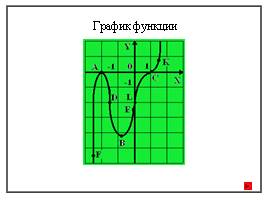
Найти область определения функции Найти первую и вторую производные f’(x),f’’(x) Найти экстремумы функции Найти все точки перегиба Установить нет ли горизонтальных и наклонных асимптот Найденные результаты по мере их получения занесем в таблицу. Перенеся их на координатную плоскость, получим общую картину графика. Добавив немногие промежуточные точки, начертим график.

1.
Функция определена и непрерывна всюду, вертикальных асимптот нет

2.
Обе производные всюду существуют

3.
Для нахождения экстремумов решаем уравнение f’(x)=0. Находим критические значения: Находим соответствующие значения функции: При переходе через f’(x) меняет знак, значит эти точки - точки экстремумы

4.
Для нахождения точек перегиба решаем Уравнение f’’(x)=0. Получаем найденное прежде значение и, кроме того, Найдем соответствующие значения функции и ее первой производной: При переходе через f’’(x) меняет знак, Значит эти точки – точки перегиба

5.
Горизонтальных и наклонных асимптот нет, так как при

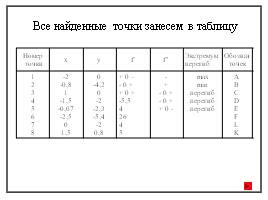
Все найденные точки занесем в таблицу
Номер точки x y f’ f’’ Экстремум перегиб Обознач точек
1 2 3 4 5 6 7 8 -2 -0,8 1 -1,5 -0,07 -2,5 0 1,5 0 -4,2 0 -2 -2,3 -5,4 -2 0,8 + 0 – - 0 + + 0 + -5,5 4 26 4 5 - + - 0 + - 0 + + 0 - max min перегиб перегиб перегиб A B C D E F L K

График функции

Вычислите производную функции
при
1) 2) 3) 4)

Найдите при каких значениях производная функции равна 0.
1) 2)
3) 4)

Найдите точки экстремума функции
1) 3; -1 2) 0;4 3) -6,5;0,5 4) -4;1

Самостоятельная работа
Постройте график функции Докажите, что функция убывает на R. Найдите наибольшее и наименьшее значение функции на [0;100] 4. Основанием прямоугольного параллеле-пипеда служит квадрат, а каждая боковая грань имеет периметр 6.Найдите параллелепипед с наибольшим объемом