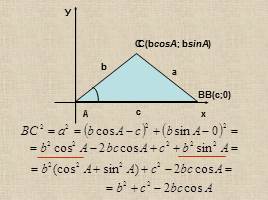Презентация - Теорема синусов - Теорема косинусов

Теорема синусов. Теорема косинусов.
МАОУ «СОШ № 2» г. Стерлитамак, РБ Учитель Ибрагимова Гузель Галинуровна

Теорема синусов
Геометрия 9 класс

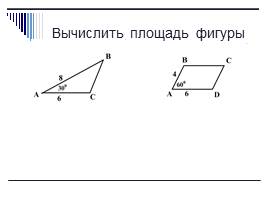
Вычислить площадь фигуры

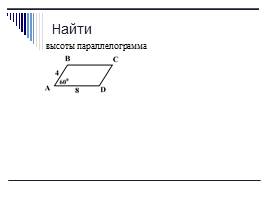
Найти
высоты параллелограмма

Теорема синусов
Формулировка. Стороны треугольника пропорциональны синусам противолежащих углов.
С
b
a
c
A
B
a
sin A
b
sin B
c
sin C
=
=

Доказательство
Дано: АВС ВС = а, СА = b, АВ = с Доказать:
a
sin A
b
sin B
c
sin C
=
=
С
b
a
c
A
B
Доказательство:

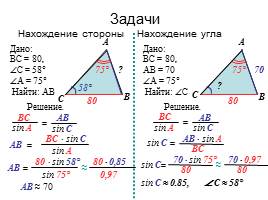
Задачи
Нахождение стороны
Нахождение угла
Дано: ВС = 80, С = 58° А = 75° Найти: АВ
Дано: ВС = 80, АВ = 70 А = 75° Найти: С
С
58°
80
?
A
B
75°
С
75°
80
70
A
B
?
Решение.
Решение.
ВС
sin A
АВ
sin C
=
АВ
=
80
∙ sin 58°
sin 75°
АВ
=
ВС
∙ sin С
sin А
≈
80 ∙ 0,85
0,97
АВ ≈ 70
ВС
sin A
АВ
sin C
=
sin C
ВС
АВ ∙ sin A
=
sin C
80
70 ∙ sin 75°
=
80
70 ∙ 0,97
≈
sin C ≈ 0.85,
 С ≈ 58°

С
b
a
c
A
B
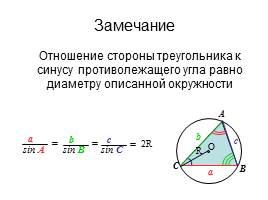
Замечание
Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности
a
sin A
b
sin B
c
sin C
=
=
=
2R
R
О

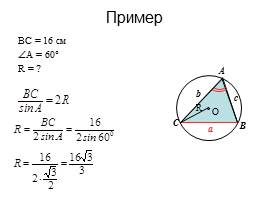
Пример
ВС = 16 см А = 60° R = ?
O
С
b
a
c
A
B
R

В треугольнике АВС, угол В равен 45°, угол С равен 15°, сторона АС равна 6 см. Найдите сторону ВС.
ΔАВС: ΔMNP: … ΔDOC: … ΔKPS: …
Запишите теорему синусов для треугольников:

Теорема
косинусов
К
В
М
?

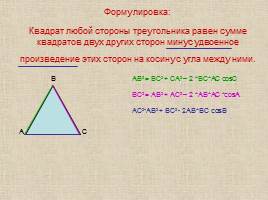
Формулировка: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
АВ2 = ВС2 + СА2 – 2 *ВС*АС cosС ВС2 = АВ2 + АС2 – 2 *АВ*АС *cosА АС2=АВ2 + ВС2 - 2АВ*ВС cosВ

Доказательство теоремы

х
У
А
С
В(c;0)
b
a
c
С(bcosA; bsinA)
B

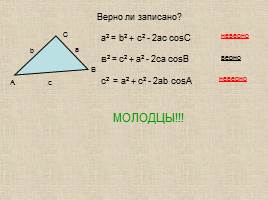
Верно ли записано?
а2 = b2 + с2 - 2aс cosC в2 = с2 + a2 - 2сa cosB с2 = a2 + c2 - 2ab cosA
неверно
верно
неверно
МОЛОДЦЫ!!!

Ключевые задачи

4
4
5
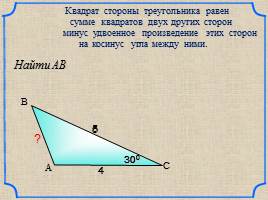
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
на косинус угла между ними.
минус удвоенное произведение этих сторон
С
А
В
5
5
300
300
?
4
Найти АВ

4
С
А
В
?
Найти угол В
2
 
 
 
 

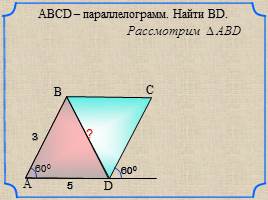
600
5
5
3
3
3
5
?
600
D
A
B
C
ABСD – параллелограмм. Найти ВD.
600

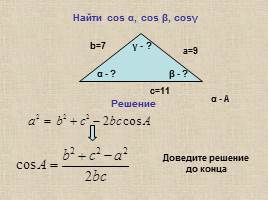
Найти cos α, cos β, cosγ
b=7
a=9
c=11
α - ?
β - ?
γ - ?
Решение
α - А
Доведите решение до конца

Применение теоремы косинусов
Нахождение стороны треугольника (знаем две стороны, угол между ними)
Вид треугольника по углам (знаем все стороны треугольника)
Угол треугольника (косинус угла) (знаем все стороны треугольника)
Медианы треугольника (знаем все стороны треугольника)

Верно ли записаны формулировки?
1. Квадрат стороны треугольника равен сумме квадратов всех сторон минус удвоенное произведение любых двух сторон на косинус угла между ними. 2. Квадрат стороны треугольника равен сумме квадратов двух других сторон на синус угла между ними. 3. Квадрат стороны трапеции равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. 4. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
НЕВЕРНО
НЕВЕРНО
НЕВЕРНО
ВЕРНО