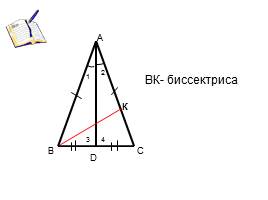Слайды и текст этой онлайн презентации
Слайд 1
УРОК ГЕОМЕТРИИ 7класс
Слайд 2
Кто ничего не замечает, Тот ничего не изучает. Кто ничего не изучает, Тот вечно хнычет и скучает.
Девиз нашего урока:
“Есть в математике нечто, вызывающее человеческий восторг”
Слайд 3
СВОЙСТВА
РАВНОБЕДРЕННОГО
ТРЕУГОЛЬНИКА
ТЕМА УРОКА
Слайд 5
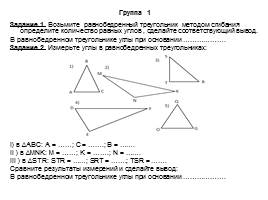
Группа 1
Задание 1. Возьмите равнобедренный треугольник методом сгибания определите количество равных углов , сделайте соответствующий вывод.
В равнобедренном треугольнике углы при основании ……………….
Задание 2. Измерьте углы в равнобедренных треугольниках:
I) в ∆АВС: А = ……; С = …….; В = …….
II ) в ∆MNK: M = ……; K = …….; N = …….
III ) в ∆STR: STR = ……; SRT = …….; TSR = …….
Сравните результаты измерений и сделайте вывод:
В равнобедренном треугольнике углы при основании ……………….
Слайд 6
Группа 2
Задание 1.
1. Начертите равнобедренный Δ АВС с основанием ВС
2. С помощью транспортира и линейки проведите из вершины А к стороне ВС биссектрису выделите её красным цветом.
3. С помощью масштабной линейки проведите медиану из вершины А выделите её зелёным цветом.
4. С помощью треугольника проведите высоту из вершины А выделите синим цветом .Что вы заметили? Сделайте вывод:
В равнобедренном треугольнике биссектриса, проведенная к основанию, является ………………… и …………………….
Слайд 7
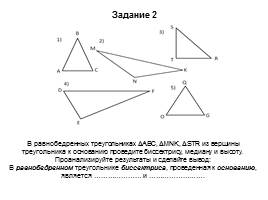
Задание 2
В равнобедренных треугольниках ΔАВС, ΔMNK, ΔSTR из вершины треугольника к основанию проведите биссектрису, медиану и высоту. Проанализируйте результаты и сделайте вывод:
В равнобедренном треугольнике биссектриса, проведенная к основанию, является ………………… и …………………….
Слайд 8
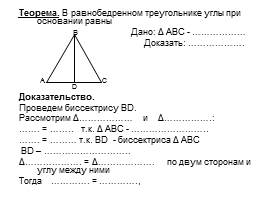
Теорема. В равнобедренном треугольнике углы при основании равны
Дано: Δ АВС - ………………
Доказать: ……………….
Доказательство.
Проведем биссектрису ВD.
Рассмотрим Δ……………… и Δ…………….:
……. = …….. т.к. Δ АВС - ……………………..
……. = ……… т.к. ВD - биссектриса Δ АВС
ВD – ………………………..
Δ………………. = Δ………………. по двум сторонам и углу между ними
Тогда …………. = ………….,
Слайд 9
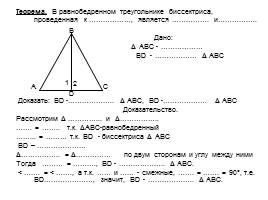
Теорема. В равнобедренном треугольнике биссектриса, проведенная к ………………, является ……………. и……………..
Дано:
Δ АВС - ………………
ВD - ……………… Δ АВС
Доказать: ВD -……………….. Δ АВС, ВD -………………. Δ АВС
Доказательство.
Рассмотрим Δ …………... и Δ……………..
……. = …….. т.к. ΔАВС-равнобедренный
……... = ……… т.к. ВD - биссектриса Δ АВС
ВD – …………………
Δ…………….. = Δ…………… по двум сторонам и углу между ними
Тогда ……… = ………., ВD - ……………….. Δ АВС.
< ……. = < ……., а т.к. …… и …… - смежные, ……. = ……. = 90°, т.е. ВD…………………, значит, ВD - ……………….. Δ АВС.
1
2
Слайд 10
А
ВК- биссектриса
К
Слайд 11
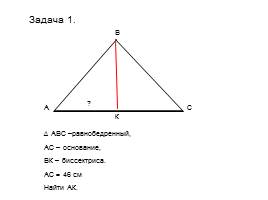
∆ АВС –равнобедренный,
АС – основание,
ВК – биссектриса.
АС = 46 см
Найти АК.
Задача 1.
С
К
?
В
А
Слайд 12
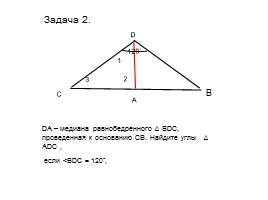
Задача 2.
DA – медиана равнобедренного ∆ ВDС, проведенная к основанию СВ. Найдите углы ∆ АDС ,
если
Слайд 13
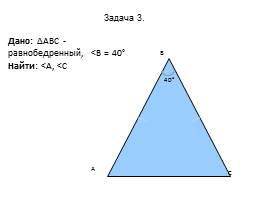
40°
A
B
C
Дано: ∆АВС - равнобедренный,
Задача 3.
Слайд 14
50°
М
N
P
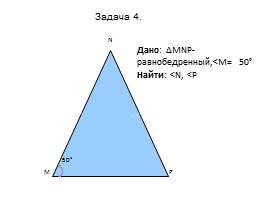
Дано: ∆MNP- равнобедренный,<М= 50°
Найти:
Задача 4.
Слайд 15
Где в жизни встречаются равнобедренные треугольники?
Слайд 22
Домашнее задание:
Пункт 18 (2);
№ 70 в рабочей тетради;
Творческое задание:
Из 6 спичек получить 4 равносторонних треугольника.
Слайд 23
Теоретический тест
1.Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
2. Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является медианой и биссектрисой.
3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
5. Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая ее медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
 Теоретический тест «Свойства медианы равнобедренного треугольника»
Теоретический тест «Свойства медианы равнобедренного треугольника» Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Некоторые свойства прямоугольных треугольников
Некоторые свойства прямоугольных треугольников Определение и свойства медианы прямоугольного треугольника
Определение и свойства медианы прямоугольного треугольника Построение равнобедренного треугольник по длине его основания и боковой стороне
Построение равнобедренного треугольник по длине его основания и боковой стороне Равнобедренный треугольник
Равнобедренный треугольник Решение задач по теме «Прямоугольный треугольник»
Решение задач по теме «Прямоугольный треугольник»