Презентация - Решение квадратного неравенства с помощью графика квадратичной функции
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 83%
- Слайдов: 15
- Просмотров: 3506
- Скачиваний: 886
- Размер: 0.24 MB
- Класс: 8
- Формат: ppt / pptx
Примеры похожих презентаций
Алгебра. Квадратичная функция. Функция. Функция у = kx², ее свойства и график
План построения графика квадратичной функции
Квадратное неравенство и его решение
Построение графиков функции с помощью электронной таблицы Excel
Квадратичная функция, ее график и свойства
Функция квадратного корня, её свойства и график
Построение графика квадратичной функции
Слайд 1
Решение квадратного неравенства с помощью графика квадратичной функции
8 класс
Айнетдинова Х. А. МОУ Петряксинская СОШ
8 класс
Айнетдинова Х. А. МОУ Петряксинская СОШ
Слайд 2
Алгоритм решения квадратного неравенства с помощью графика:
определить направление ветвей параболы по знаку первого коэффициента квадратичной функции;
найти действительные корни соответствующего квадратного уравнения или установить, что их нет;
изобразить эскиз графика квадратичной функции, используя точки пересечения (или касания) с осью Ох, если они есть;
по графику определить промежутки, на которых функция принимает нужные значения.
Слайд 3
Алгоритм решения квадратного неравенства
на примере неравенства .
Х
5
-1
Определим направление ветвей параболы. a > 0 - ветви направлены вверх
1)
2) Найдем точки пересечения с Ох:
3) Изобразим эскиз графика
4) По графику определим промежутки, на которых функция принимает нужные значения
Ответ:
+
+
Х
5
-1
Определим направление ветвей параболы. a > 0 - ветви направлены вверх
1)
2) Найдем точки пересечения с Ох:
3) Изобразим эскиз графика
4) По графику определим промежутки, на которых функция принимает нужные значения
Ответ:
+
+
Слайд 4
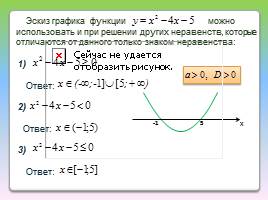
Эскиз графика функции можно использовать и при решении других неравенств, которые отличаются от данного только знаком неравенства:
1)
Ответ:
2)
Ответ:
3)
Ответ:
-1
5
Х
-1
5
Х
Слайд 5
Х
5
-1
Определим направление ветвей параболы. а < 0 - ветви направлены вниз.
1)
2) Найдем точки пересечения с Ох:
3) Изобразим эскиз графика функции
4) Выделим соответствующие части графика и соответствующие части Ох.
Решить неравенство
Ответ:
+
5
-1
Определим направление ветвей параболы. а < 0 - ветви направлены вниз.
1)
2) Найдем точки пересечения с Ох:
3) Изобразим эскиз графика функции
4) Выделим соответствующие части графика и соответствующие части Ох.
Решить неравенство
Ответ:
+
Слайд 6
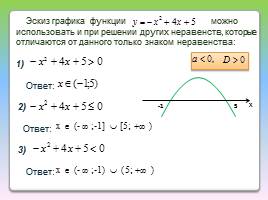
Эскиз графика функции можно использовать и при решении других неравенств, которые отличаются от данного только знаком неравенства:
1)
Ответ:
2)
Ответ:
3)
Ответ:
-1
5
Х
-1
5
Х
Слайд 7
Х
-2
а > 0 - ветви ↑.
3) Изобразим эскиз графика.
4) График не ниже оси Ох (≥).
D = 0. – точка касания.
1)
2)
Решить неравенство
a > 0, D = 0
+
+
+
-2
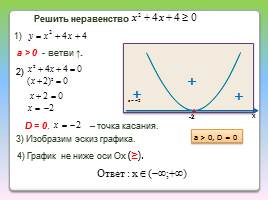
а > 0 - ветви ↑.
3) Изобразим эскиз графика.
4) График не ниже оси Ох (≥).
D = 0. – точка касания.
1)
2)
Решить неравенство
a > 0, D = 0
+
+
+
Слайд 8
Эскиз графика функции можно использовать и при решении других неравенств, которые отличаются от данного только знаком неравенства:
1)
Ответ:
2)
Ответ: Решений нет.
3)
Ответ:
-2
Х
a > 0, D = 0
-2
Х
a > 0, D = 0
Слайд 9
Х
-2
а < 0 - ветви .
3) Изобразим эскиз графика.
4) График не выше оси Ох (≤).
D = 0. – точка касания.
1)
2)
Решить неравенство
a < 0, D = 0
-
-
-
-2
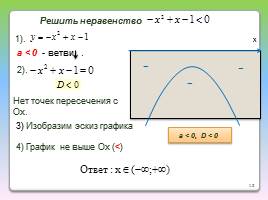
а < 0 - ветви .
3) Изобразим эскиз графика.
4) График не выше оси Ох (≤).
D = 0. – точка касания.
1)
2)
Решить неравенство
a < 0, D = 0
-
-
-
Слайд 10
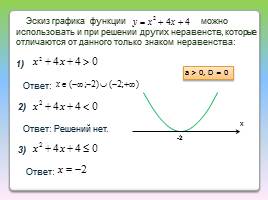
Эскиз графика функции можно использовать и при решении других неравенств, которые отличаются от данного только знаком неравенства:
1)
Ответ:
2)
Ответ: Решений нет.
3)
Ответ:
-2
Х
a < 0, D = 0
-2
Х
a < 0, D = 0
Слайд 11
11
Х
а > 0 - ветви ↑.
1).
2).
3) Изобразим эскиз графика 4) График не ниже Ох (≥)
Нет точек пересечения с Ох.
Решить неравенство
a > 0, D < 0
+
+
+
Х
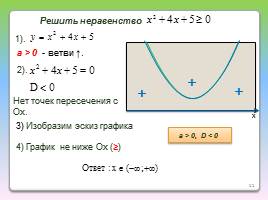
а > 0 - ветви ↑.
1).
2).
3) Изобразим эскиз графика 4) График не ниже Ох (≥)
Нет точек пересечения с Ох.
Решить неравенство
a > 0, D < 0
+
+
+
Слайд 12
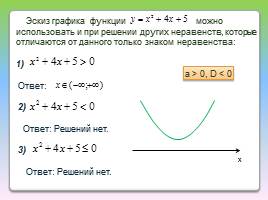
Эскиз графика функции можно использовать и при решении других неравенств, которые отличаются от данного только знаком неравенства:
1)
Ответ:
2)
Ответ: Решений нет.
3)
Ответ: Решений нет.
Х
a > 0, D < 0
Х
a > 0, D < 0
Слайд 13
13
Х
а < 0 - ветви .
1).
2).
3) Изобразим эскиз графика 4) График не выше Ох (<)
Нет точек пересечения с Ох.
Решить неравенство
a < 0, D < 0
-
-
-
Х
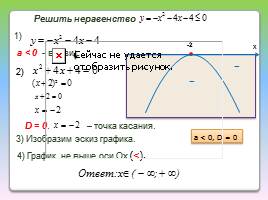
а < 0 - ветви .
1).
2).
3) Изобразим эскиз графика 4) График не выше Ох (<)
Нет точек пересечения с Ох.
Решить неравенство
a < 0, D < 0
-
-
-
Слайд 14
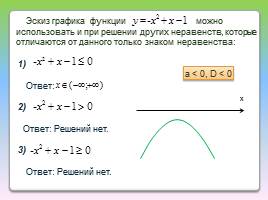
Эскиз графика функции можно использовать и при решении других неравенств, которые отличаются от данного только знаком неравенства:
1)
Ответ:
2)
Ответ: Решений нет.
3)
Ответ: Решений нет.
Х
a < 0, D < 0
Х
a < 0, D < 0
Слайд 15
Литература
Алгебра: Учеб. Для 8 кл. общеобразоват. учреждений/ Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. – М.: Просвещение
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.