Презентация - Решение нестандартных задач на движение

ДВИЖЕНИЕ

Даны выражения: 1) 2) 3) Какие из этих выражений не имеют при а=0 смысла? 1) только 1; 2) только 3; 3) 1 и 3; 4) 1, 2 и 3.
Устно

Устно
2) При каких указанных значениях x выражение не имеет смысла? 1) при х = 0; 2) при х =-6; 3) при х = -1; 4) при х =-4.

Устно
3) Автомобиль расходует а литров бензина на 100 км пути. Сколько литров бензина потребуется, чтобы проехать 37 км? 1) л; 3) л; 2) л; 4) л.

Устно
4) Из формулы при равноускоренном движении S = выразить время t. 1) t = 2) t = 3) t = 4) t =

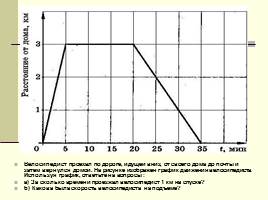
Велосипедист проехал по дороге, идущей вниз, от своего дома до почты и затем вернулся домой. На рисунке изображен график движения велосипедиста. Используя график, ответьте на вопросы : а) За сколько времени проезжал велосипедист 1 км на спуске? б) Какова была скорость велосипедиста на подъеме?

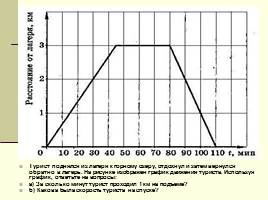
Турист поднялся из лагеря к горному озеру, отдох­нул и затем вернулся обратно в лагерь. На рисунке изображен график движения туриста. Используя гра­фик, ответьте на вопросы: а) За сколько минут турист проходил 1 км на подъеме? б) Какова была скорость туриста на спуске?

Задачи на движение
Уравнения, которые составляются на основании условий задач на движение, обычно содержат такие величины, как расстояние, скорости движущихся объектов, время, а также скорость течения воды (при движении по реке). При решении этих задач принимают следующие допущения: Если нет специальных оговорок, то движение считается равномерным. Повороты движущихся тел, переходы на новый режим движения считаются происходящими мгновенно. Если тело с собственной скоростью х движется по реке, скорость течения которой равна у, то скорость движения тела по течению считается равной (х+у), а против течения – (х-у). При решении задач на движение рекомендуется сделать рисунок, отображающий все условия задачи. При этом решающий задачу должен выбрать схему решения: какого вида уравнения составлять, то есть что сравнивать: время, затраченное на движение на отдельных участках пути, или пройденный каждым объектом путь.

При решении задач такого типа часто необходимо узнать время встречи двух объектов, начинающих движение одновременно из двух точек с разными скоростями и движущихся навстречу друг другу либо в случае, когда один объект догоняет другой.

Пусть расстояние между точками А и В равно S. Два тела начинают движение одновременно, но имеют разные скорости V1 и V2. Пусть С – точка встречи, а t – время движения тел до встречи. В случае движения навстречу друг другу имеем АС=V2t, BC= V1t. Сложим эти два равенства: АС+СВ= V2t + V1t =(V1+ V2)t  AB=S=(V1+ V2)t 

Если одно тело догоняет другое, то теперь получаем АС= V1t, BC=V2t. Вычтем эти равенства: АС–ВС=(V1–V2)t. Так как АС–ВС=AB=S, то время, через которое первое тело догонит второе, определяется равенством

3 часть. Решение задач.
Задача 1. Два велосипедиста одновременно отправляются навстречу друг другу из двух сёл. Первый мог бы проехать расстояние между сёлами за 45 минут, а второй-за 30 минут. Через какое время они встретятся?

Решение задач.
Задача 2. Из пункта А в пункт В, расположенный выше по течению реки, вышла моторная лодка. Собственная скорость лодки в пять раз больше течения реки. Одновременно навстречу ей из пункта В отправляется плот. Встретив плот, лодка сразу повернула назад и пошла вниз по течению реки. Какую часть пути от В до А пройдёт плот к моменту возвращения лодки в пункт А?