Презентация - Решение задач на движение по наклонной плоскости

Решение задач на движение по наклонной плоскости.

План решения задач по динамике
1. Сделать рисунок, на котором обозначить направление координатных осей, ускорения и всех сил, приложенных к телу .
2. Для каждого тела записать в векторном виде уравнение второго закона Ньютона, перечислив в его правой части в любом порядке все силы, приложенные к телу
3. Записать полученные в п. 2 уравнения в проекции на оси координат.
5. Найти численное значение неизвестной величины, если этого требует условие задачи.
4. Из полученного уравнения (системы уравнений) выразить неизвестную величину.

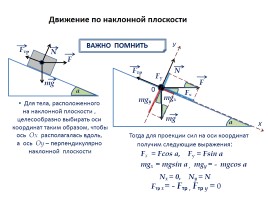
Движение по наклонной плоскости
ВАЖНО ПОМНИТЬ
mg
N
F
Fтр.
Для тела, расположенного на наклонной плоскости , целесообразно выбирать оси координат таким образом, чтобы ось Ох располагалась вдоль, а ось Оу – перпендикулярно наклонной плоскости
а
Тогда для проекции сил на оси координат получим следующие выражения:
Fх. = Fcos а, Fу = Fsin а
mgх. = mgsin а , mgу = - mgcos а
Nx = 0,
Ny = N
Fтр x= - Fтр., Fтр у = 0 .

Движение тела по наклонной плоскости без трения:

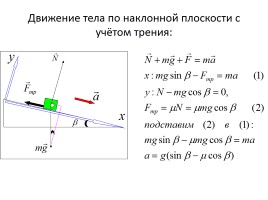
Движение тела по наклонной плоскости с учётом трения:

а
β
m1g
m2g
N1
N2
T
T
У
У
Х
Х
а
а
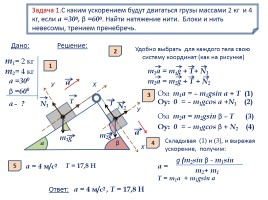
Задача 1.С каким ускорением будут двигаться грузы массами 2 кг и 4 кг, если а =300, β =600. Найти натяжение нити. Блоки и нить невесомы, трением пренебречь.
m1= 2 кг
m2= 4 кг
Дано:
а =300
β =600
а - ?
Решение:
1
2
Удобно выбрать для каждого тела свою систему координат (как на рисунке)
m1a = m1g + Т+ N1
m2a = m2g + Т + N2
3
Оx: m1a = – m1gsin а + Т (1)
Оy: 0 = – m1gcos а +N1 (2)
Оx: m2a = m2gsin β – Т (3)
Оy: 0 = – m1gcos β + N2 (4)
4
Складывая (1) и (3), и выражая ускорение, получим:
g (m2sin β - m1sin

a =
m2+ m1
Т = 17,8 H
T = m1a + m1gsin а
5
a = 4 м/с2
Ответ: а = 4 м/с2 , T = 17,8 H

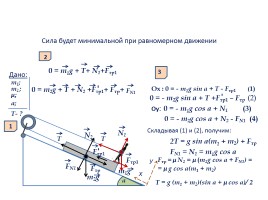
Задача2.Человек массой m1 , упираясь ногами в ящик массой m2 подтягивает его с помощью каната, перекинутого через блок, по наклонной плоскости с углом наклона а. С какой минимальной силой нужно тянуть канат, чтобы подтянуть ящик к блоку? Коэффициент трения между яиом и наклонной плоскостью μ

а
У
Х
FN1
N2
m1g
m2g
T
T
Fтр.
Fтр1.1
1
Дано:
m1;
m2 ;
μ;
а;
T- ?
Сила будет минимальной при равномерном движении
2
0 = m1g + Т+ N1+Fтр1
0 = m2g + Т + N2 +Fтр1+ Fтр+
3
Ох : 0 = - m1g sin а + Т - Fтр1 (1)
0 = - m2g sin а + Т +Fтр1 – Fтр (2)
Оу: 0 = - m1g cos а + N1 (3)
0 = - m2g cos а + N2 - FN1 (4)
N1
FN1 = N1 = m1g cos а
Складывая (1) и (2), получим:
2Т = g sin а(m1 + m2) + Fтр
Fтр = μ N2 = μ (m2g cos а + FN1) = = μ g cos а(m1 + m2)
Т = g (m1 + m2)(sin а + μ cos а)/ 2
FN1

а
Х
FN1
N2
m1g
m2g
T
1
У
T
Fтр.1
N1
Задача 3. К концам троса, перекинутого через блок, привязаны бруски с массами m1= m и m2 = 4m, находящиеся на гладкой наклонной плоскости с углом наклона 300. При каком минимальном значении коэффициента трения между брусками они будут покоиться?
m1= m
m2 = 4m
а = 300
μ - ?
Дано:
Решение:
m1a = m1g + Т+ N1+Fтр
m2a = m2g + Т + N2 +Fтр+ FN1
Ох : 0 = - m1g sin а + Т- Fтр (1)
0 = - m2g sin а + Т +Fтр (2)
Оу: 0 = - m1g cos а + N1 (3)
0 = - m2g cos а + N2 - FN1 (4)
Из (3): N1 = m1g cos а
Из (4): N2 = m2g cos а + FN1
N1 = FN1 , поэтому N2 = m2g cos а - m1g cos а
Вычтем из (1) (2) и учитывая, что
Fтр = Fтр
получим:
2
2 Fтр = m2g sin а - m1g sin а
Fтр = μ N1 = μ m1g cos а
μ =
m2g sin а - m1g sin а
2m1g cos а
3 tgа
=
2
3
4
5

Задача 4.Д/з На наклонную плоскость с углом наклона 300 положили кирпич массой2кг. Коэффициент трения скольжения между поверхностями равен 0,8. Чему равна сила трения, действующая на кирпич?