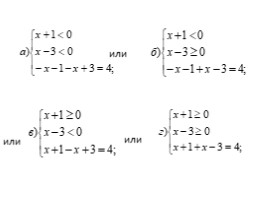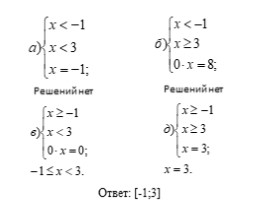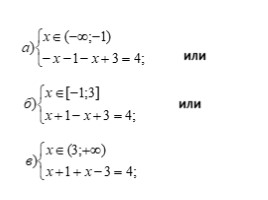Слайды и текст этой онлайн презентации
Слайд 1
Решение уравнения с модулем
Родионова Г. М., учитель математики МБУ «Школа №82» г.о.Тольятти
Слайд 2
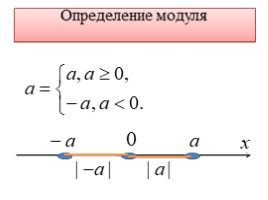
Определение модуля
Слайд 3
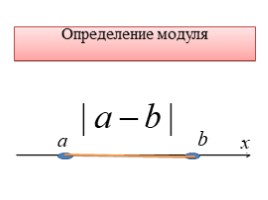
Определение модуля
Слайд 4
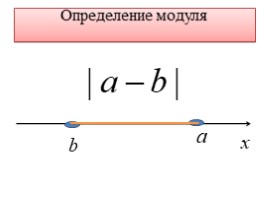
Определение модуля
Слайд 6
Решение уравнений с модулем
Слайд 7
Решение уравнений с модулем
Слайд 8
Уравнение с модулем
Решить уравнение
Решение:
Для раскрытия двух модулей рассмотрим
следующие 4 случая:
Найдем нули
подмодульных
выражений
I способ.
Слайд 10
Решений нет
Решений нет
Ответ: [-1;3]
Слайд 11
Решите уравнение
II способ.
Так как обе части уравнения неотрицательные,
то при возведении их в квадрат получим
уравнение равносильное данному.
Из определения модуля следует. Что последнее
равенство выполнимо, если
т.е. когда
Ответ: [-1;3]
Слайд 12
III способ - графический
Перепишем данное уравнение в
следующем виде:
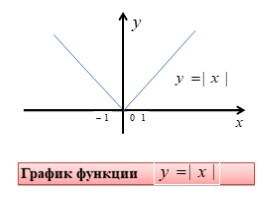
Далее изобразим графики функций
И укажем абсциссы их общих точек.
Графики совпадают при
Ответ:
Слайд 13
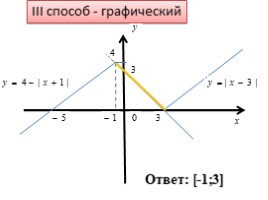
III способ - графический
Ответ: [-1;3]
Слайд 14
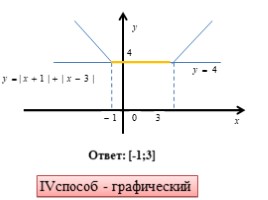
IVспособ - графический
Найдем абсциссы общих точек графика
функции
и прямой
Для построения первого графика
достаточно взять несколько точки
с абсциссами х < 1 и x > 3, после
чего последовательно соединить их до
получения ломаной.
Слайд 15
Ответ: [-1;3]
IVспособ - графический
Слайд 16
V способ
Числа -1 и 3 разбивают числовую прямую на
Три интервала, на каждом из которых
подмодульные выражения имеют определенный знак.
Найдем решение уравнения в каждом из
полученных промежутков:
Слайд 18
Нет решения
Ответ: [-1;3]
Слайд 19
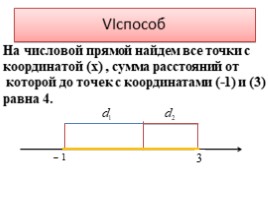
VIспособ
На числовой прямой найдем все точки с
координатой (х) , сумма расстояний от
которой до точек с координатами (-1) и (3)
равна 4.
Слайд 20
Литература:
Алгебра 9кл: учеб. для общеобразоват. учреждений/
Мордкович А.Г .– М.: Мнемозина, 2017.
Журнал «Математика в школе» №3,2010 , стр.31.
Алгебра: Нестандартные задачи: экспресс-
репетитор для подготовки к ГИА: 9-й кл./Г.В.
Сычева, Н.В. Гусева,В.А. Гусев,-М.:АСТ:Астрель
; Владимир: ВКТ, 2010
 Решение неполного уравнения третьей степени
Решение неполного уравнения третьей степени Тригонометрия. Решение уравнений
Тригонометрия. Решение уравнений Решение систем уравнений второй степени урок закрепления знаний. Борисова в.С. Учитель математики мбоу сош №11
Решение систем уравнений второй степени урок закрепления знаний. Борисова в.С. Учитель математики мбоу сош №11 Открытый урок по математике. Графический метод решения систем уравнений с двумя переменными
Открытый урок по математике. Графический метод решения систем уравнений с двумя переменными Решение задач с помощью уравнений
Решение задач с помощью уравнений Урок 3 класс. Урок – путешествие. Мифы древней греции «решение уравнений»
Урок 3 класс. Урок – путешествие. Мифы древней греции «решение уравнений» Математика 1 класс «Решение уравнений с неизвестным вычитаемым а - х = б»
Математика 1 класс «Решение уравнений с неизвестным вычитаемым а - х = б»