Презентация - Функции их свойства и графики
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 85%
- Слайдов: 42
- Просмотров: 5851
- Скачиваний: 3409
- Размер: 0.46 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Алгебра. Квадратичная функция. Функция. Функция у = kx², ее свойства и график
Алгебра. Квадратичная функция. Функция. Функция у = kx², ее свойства и график Урок алгебры по теме «Функция y=ax², её график и свойства» с применение системы учебных заданий как средства достижения планируемых результатов ФГОС. 9-й класс
Урок алгебры по теме «Функция y=ax², её график и свойства» с применение системы учебных заданий как средства достижения планируемых результатов ФГОС. 9-й класс Функция её свойства и график
Функция её свойства и график … По улицам Архангельска. Линейная функция, её график и свойства
… По улицам Архангельска. Линейная функция, её график и свойства Свойства и графики Тригонометрических функций
Свойства и графики Тригонометрических функций Степенная функция с натуральным и целым показателем. Ее свойства и график
Степенная функция с натуральным и целым показателем. Ее свойства и график Квадратичная функция, ее график и свойства
Квадратичная функция, ее график и свойства
Слайды и текст этой онлайн презентации
Слайд 1

Функции их свойства
и графики Что такое «функция»? Способы задания функции. Схема исследования функции.
Слайд 2

Определение функции. Функцией называется зависимость между двумя переменными (У и Х), в которой каждому значению независимой переменной (Х) соответствует единственное значение зависимой переменной (У). Независимую переменную называют - аргумент . Значения зависимой переменной называют значениями функции . Запись У f (X) читается: У – функция от Х.
Слайд 3
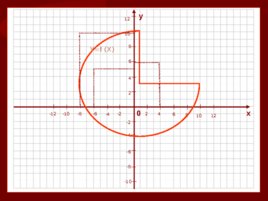
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 У f (X)
Слайд 4

Способы задания функции. Графически. С помощью формулы. Таблицей. Словесный. Рекуррентный.
Слайд 5
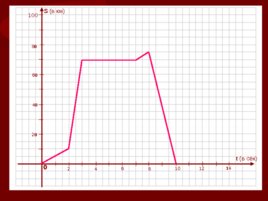
t (в сек) 4 2 2 0 4 0 1 4 6 6 0 8 8 0 10 100 12 S (в км) 0
Слайд 6
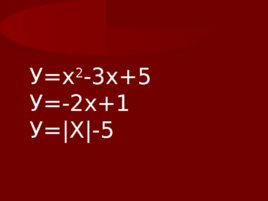
У х 2 -3х 5 У -2х 1 У X -5
Слайд 7

День недели Дежурные Понедельник Иванова А Вторник Петров Д Среда Сидорова К Четверг Козлов М Пятница Никитин Е Суббота Макарова Т
Слайд 8

Каждому натуральному числу поставим в соответствие его квадрат.
Слайд 9

а 1 3,
а n 1 2 а n -1.
Слайд 10

1. Область определения Все значения независимой переменной образуют область определения функции -D (f). Значения независимой переменной находятся на оси абсцисс (Ох)
Слайд 11
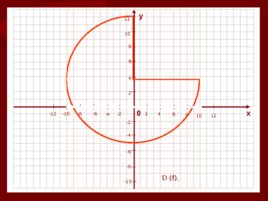
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 D (f).
Слайд 12

Если функция задана формулой и не указана ее область определения, то область определения функции состоит из всех значений аргумента, при которых формула имеет смысл. Укажите область определения функций: а) , б) , в)
Слайд 13

2. Область значений функции. Все значения, которые принимает зависимая переменная, образуют область значений функции – E (f). Значения зависимой переменной находятся на оси ординат (Оу) Единственная область, которая записывается по оси Оу
Слайд 14
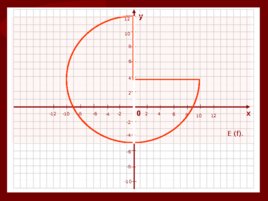
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 E (f).
Слайд 15
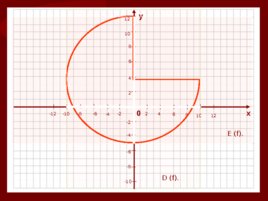
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 D (f). E (f).
Слайд 16

3. Промежутки знакопостоянства у 5х 2-3 х-2 график парабола, ветви вверх Решите неравенство: 5х 2-3 х-2 0 Х1 -0,4; х2 1 (- ;-0,4) U(1 ; ) решение выше оси Ох 3. 1 . Значения функции положительны. У 0 участки графика лежа т выше оси Ох
Слайд 17
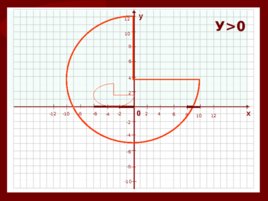
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 У 0
Слайд 18

3. Промежутки знакопостоянства у 5х 2-3 х-2 график парабола, ветви вверх Решите неравенство: 5х 2-3 х-2 0 Х1 -0,4; х2 1 (-0,4;1) решение ниже оси Ох 3.2. Значения функции отрицательны. У участки графика лежа т ниже оси Ох
Слайд 19
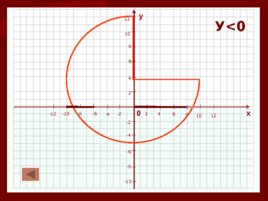
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 У
Слайд 20

Промежутки знакопостоянства 3.3. Значения функции равны нулю. Нули функции - т очки пересечения с осями координат Пересечение с осью Ох: У 0 (х;0) Пересечение с осью Оу: Х 0 (0;у) Если функция задана формулой, то промежутки знакопостоянства можно найти решив неравенство или уравнение (для нулей функции)
Слайд 21
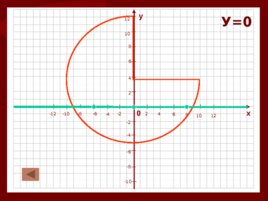
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 У 0
Слайд 22

4. Монотонность функции промежутки возрастания и убывания функции 4.1. Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции. График «идет вверх/вниз» при движении слева направо по оси Ох
Слайд 23
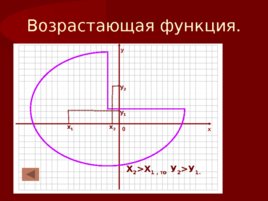
-10 х у 0 Возрастающая функция. х 1 х 2 у 1 у 2 Х 2 Х 1 , то У 2 У 1.
Слайд 24

4. Монотонность функции промежутки возрастания и убывания функции 4.2. Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. График «идет вверх/вниз» при движении слева направо по оси Ох
Слайд 25
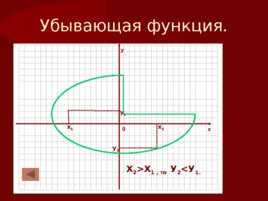
-10 х у 0 Убывающая функция. х 1 х 2 у 1 у 2 Х 2 Х 1 , то У 2 У 1.
Слайд 26
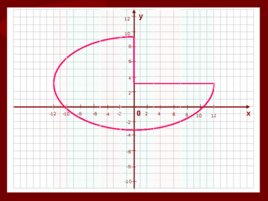
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12
Слайд 27

5. Четные и нечетные функции. 5.1. Функция у f (x) называется четной, если для всех х из области определения функции для противоположных аргументов значения функции одинаковые. Выполняется равенство f (-x) f (x). График четной функции симметричен относительно оси Оу
Слайд 28
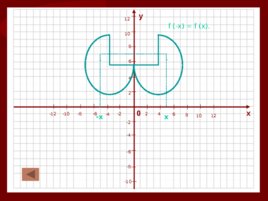
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 -х х f (-x) f (x).
Слайд 29

5. Четные и нечетные функции. 5.2. Функция у f (x) называется нечетной, если для всех х из области определения функции для противоположных аргументов значения функций противоположные. Выполняется равенство f (-x) - f (x). для того чтобы определить четность или нечетность функции по формуле, вместо х подставить –х и выяснить знак выражения после подстановки № 74 (а-г), 75(а-г) График нечетной функции симметричен относительно начала координат
Слайд 30
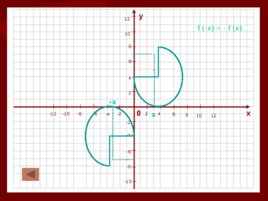
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12 -х х f (-x) - f (x).
Слайд 31

6. Ограниченность функции. 6.1. Функция y f (x) называется ограниченной снизу, если для любого х из области определения функции выполняется условие f (x) a , где а – некоторое число. График лежит выше прямой у а ограниченность функции можно посмотреть по области значений функции
Слайд 32
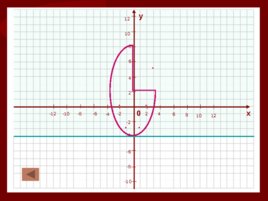
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12
Слайд 33

6. Ограниченность функции. 6 .2 Функция y f (x) называется ограниченной сверху, если для любого х из области определения функции выполняется условие f (x) b , где b – некоторое число. График лежит ниже прямой у b
Слайд 34
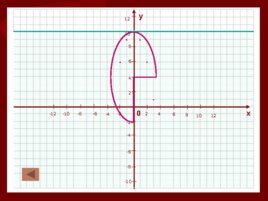
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12
Слайд 35

6. Ограниченность функции. 6.3. Функция называется ограниченной, если она ограничена и снизу, и сверху.
Слайд 36
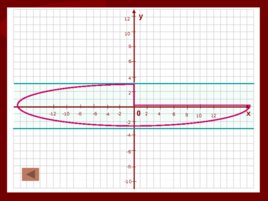
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12
Слайд 37
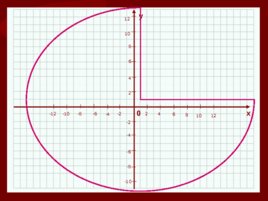
0 х у 4 2 2 -2 -2 -4 -4 4 6 -6 -6 6 8 -8 -8 8 10 -10 -10 10 12 -12 12
Слайд 38

7. Наибольшее и наименьшее значение функции на промежутке это самая высокая и самая низкая точки на графике (ответ записывается в виде координаты у)
Слайд 39

8. Точки максимума, минимума и перегиб. (х;у) Мах – самая высокая точка Min – самая низкая точка Перегиб – это волна или резкая смена направления
Слайд 40

9. Непрерывность функции. Функция называется непрерывной, если у нее нет точек разрыва
Слайд 41
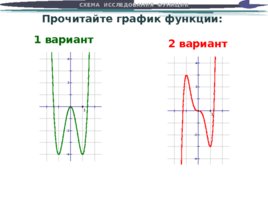
Прочитайте график функции: 1 вариант 2 вариант СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
Слайд 42

Прочитайте график функции: 1. Область определения функции D(y) (- ; ) 2. Область значений функции E(y) (-4 ; ) E(y) (- ; ) 3. Чётность/нечетность функции Чётная Нечётная 4. Нули функции у 0 при х 0; 1,4 у 0 при х 0; 1,2 5. Промежутки возрастания/ убывания функции y при х –1;0 , 1; y при (– ;–1 , 1; y при x (– ;-1 , 0;1 y при х x –1; 1 6. Наибольшее/наименьшее значение функции унаим –4; унаиб не сущ. Унаим , унаиб не сущ. 7. Ограниченность функции Ограничена снизу Не ограничена 8. Непрерывность функции непрерывна 1 вариант 2 вариант СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
