Презентация - Лекция 4. Z-преобразование

Лекция 4. Z-преобразование Вопросы лекции: Прямое Z-преобразование. Связь с преобразованием Лапласа. Литература: Гадзиковский В. И. Цифровая обработка сигналов. Учеб. пособие. – М.: СОЛОН-ПРЕСС, 2013 Электронный ресурс . Точка доступа: Сергиенко Ф. Б. Цифровая обработка сигналов. СПб.: Питер, 2002. – 608 с.

1. Прямое Z-преобразование Смысл z-преобразования заключается в том, что последовательности чисел x(k) ставится в соответствие функция комплексной переменной z, определяемая следующим образом: (4.1) Разумеется, функция X(z) определена только для тех значений z, при которых ряд (4.1) сходится. Z-преобразование играет для дискретных сигналов и систем такую же роль, как пре-образование Лапласа — для аналоговых. Определяющим при этом является тот факт, что, z-преобразование импульсной характеристики дискретной системы является дробно-рациональной функцией переменной Z.

В таблице 4.1 представлены z-изображения некоторых числовых последовательностей:

Примеры вычисления z-преобразования Вычислим z-преобразование для некоторых часто встречающихся на практике дискретных сигналов. Единичная импульсная функция Единичная импульсная функция является дискретным аналогом дельта-функции и представляет собой одиночный отсчет с единичным значением: Расчет его z-преобразования не представляет сложности: Функция X 0 (z) сходится на всей комплексной плоскости .

Единичный скачок Дискретный единичный скачок по смыслу полностью соответствует своему аналоговому прообразу. Используя определение z-преобразования (4.1), получаем (4.2) Дискретная экспоненциальная функция Дискретная экспоненциальная функция определяется следующим образом :

Для вычисления z-преобразования нужно вычислить сумму следующего ряда: Дискретная затухающая синусоида Последняя из рассматриваемых здесь дискретных последовательностей представляет собой отсчеты синусоиды с произвольными частотой и начальной фазой и экспоненциально меняющейся амплитудой: Для вычисления z-преобразования можно представить косинус по формуле Эйлера в виде полу-суммы двух комплексных экспонент, а потом воспользоваться уже готовым результатом (таблица 4.1):

2. Связь с преобразованием Лапласа Дискретное z-преобразование очень просто связано с преобразованиями Лапласа и Фурье. Рассмотрим последовательность, определенную как x(k) , и сопоставим ей временной сигнал в виде набора дельта-функций: (4.3) где T 1/f — интервал дискретизации. Преобразование Лапласа для сигнала равно: Воспользовавшись фильтрующим свойством дельта-функции, получим: (4.4)

Эта формула представляет дискретное преобразование Лапласа (ДПЛ) решётчатой функции x n , в которой q p T σ jωТ — комплексная переменная. Эта формула переходит в выражение (1), определяющую z-преобразование, если выполнить подстановку z e q e p T . Характерной особенностью ДПЛ является то, что комплексный аргумент q входит в изображение X(q) в виде показателя экспоненты e q . Но комплексная экспонента e q является периодической функцией в Q-плоскости с периодом, равным 2πj , т.е. e q j2πk e q , где k — произвольное целое число, поэтому изображение X(q) решётчатой функции x n полностью определяется в любой полосе Q -плоскости шириной 2π , параллельной вещественной оси. Обычно эта полоса выбирается симметрично по отношению к вещественной оси, как показано на рис. 1,б, и называется основной.

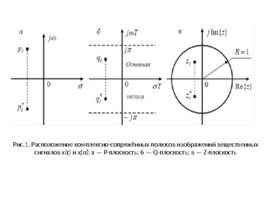
Рис.1. Расположение комплексно-сопряжённых полюсов изображений вещественных сигналов x(t) и x n : a — P-плоскость; б — Q-плоскость; в — Z-плоскость

При Re(q) σ0T функция X (q) может иметь особые точки — полюсы, в которых X(q) обращается в бесконечность. Если решётчатая функция x n является вещественной, то в симметричной относительно оси σT полосе каждому комплексному полюсу q i σ i T jω i T функции X(q) соответствует комплексно-сопряжённый полюс q i σ i T-jω i T . Для комплексных решётчатых функций x n это утверждение не справедливо. ДПЛ позволяет производить над разностными уравнениями такие же алгебраические действия, какие допускает обычное преобразование Лапласа над интегро-дифференциальными уравнениями. Однако проведение алгебраических действий над ДПЛ неудобно из-за того, что в выражении X(q) фактическим аргументом является экспонента e q . Для устранения этого недостатка вводится новая комплексная переменная z e q e p T exp(σT jωT ) (4.5)

Замена комплексной переменной приводит к отображению одной комплексной плоскости в другую. При замене (4.5) левая полуплоскость P-плоскости и левая часть основной полосы Q-плоскости преобразуются в круг единичного радиуса с центром в начале координат (рис. 1, в). С учётом обозначения (4.5) формулу (4.4) перепишем в виде (4.6) Полученное выражение является главной частью ряда Лорана, Лорана, представляющего функцию X(z) в Z -плоскости. Функция комплексного аргумента X(z) есть одностороннее Z -преобразование или просто Z -преобразование решётчатой функции x n . Если оригиналы x(t) и x n являются вещественными функциями, то комплексным полюсам их изображений X(p) в P -плоскости, X(q) в Q -плоскости и X(z) в Z -плоскости соответствуют комплексно-сопряжённые полюсы в этих плоскостях (на рис.1 полюсы p i и p i , q i и q i , z i и z i ). В случае же комплексных оригиналов x(t) и x n это свойство не выполняется.

Как видно из сопоставления выражений (4.5), (4.4) и (4.6), z -преобразование тесно связано с ДПЛ и прямо вытекает из него. Вследствие замены переменной (4.4) выражения X(z) выглядят проще, чем X(q) , к тому же изображения X(z) однозначны и в большинстве практически важных случаев имеют дробно-рациональный вид. По этой причине аппарат Z -преобразований получил более широкое распространение для описания дискретных систем, чем аппарат ДПЛ. Таким образом, взаимное соответствие между z-преобразованием X(z) и преобразованием Лапласа S(p) описывается следующим образом: . Похожими формулами описывается и связь z -преобразования X(z) с преобразованием Фурье S(ω) (заметим, что при рассмотрении этой связи нет необходимости считать последовательность односторонней):