Презентация - инейные дискретные системы с постоянными параметрами

Лекция 6. Линейные дискретные системы с постоянными параметрами Вопросы лекции: Понятие линейной дискретной системы с постоянными параметрами. Импульсная характеристика. Устойчивость дискретных систем.

1. Понятие линейной дискретной системы с постоянными параметрами. Дискретный фильтр (система) — это произвольная система обработки дискретного сигнала, обладающая свойствами линейности и стационарности. Под этими свойствами понимается то же, что и в аналоговом случае: линейность означает, что выходная реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности, а стационарность — что задержка входного сигнала приводит лишь к такой же задержке выходного сигнала, не меняя его формы. Любой фильтр обладает определенной частотной характеристикой. Чтобы она была нетривиальной, то есть чтобы коэффициент передачи фильтра на разных частотах был разным, выходной сигнал фильтра y(k) должен зависеть от нескольких отсчетов входного сигнала x(k) . Таким образом, дискретный фильтр должен обладать памятью. Чтобы обеспечить линейность и стационарность, производимые фильтром математические операции должны ограничиваться сложением и умножением на константы.

Рассмотрим простейший пример. Пусть выходной сигнал фильтра равен сумме двух последних отсчетов входного сигнала: Убедимся в том, что эта система по-разному пропускает на выход сигналы разных частот: подадим на вход фильтра серию одинаковых отсчетов (то есть сигнал нулевой частоты) (рис.1), сигнал с частотой Найквиста (рис.2) и с половинной частотой Найквиста (рис.3): рис. 1 рис. 2 рис. 3

Рассмотренный пример представляет собой простейший случай нерекурсивного фильтра . Такие фильтры суммируют некоторое число входных отсчетов, умножая их при этом на постоянные весовые коэффициенты. Теперь заметим, что помимо выходных отсчетов мы можем использовать для вычислений и ранее рассчитанные значения выходного сигнала. Попробуем просто суммировать входной отсчет и предыдущий выходной отсчет: Подаем на вход постоянный сигнал (начальное состояние фильтра считаем нулевым) (рис. 4): рис. 4

Выходной сигнал будет линейно нарастать, что рано или поздно приведет к переполнению разрядной сетки вычислительного устройства. Это сразу же демонстрирует нам главную отличительную черту фильтров, использующих при вычислениях предыдущие отсчеты выходного сигнала (их называют рекурсивными фильтрами ) — из-за наличия обратных связей они могут быть неустойчивыми. Если уменьшить влияние обратной связи, разделив предыдущий отсчет выходного сигнала на 2: Теперь выходной сигнал с уменьшающейся скоростью стремится к значению 2. Таким образом, переходный процесс в фильтре является бесконечным. Это еще одна отличительная черта рекурсивных фильтров. Итак, рекурсивные фильтры суммируют при расчетах не только входные, но и некоторое количество предыдущих выходных отсчетов сигнала, умножая их при этом на постоянные весовые коэффициенты.

Разностное уравнение ЦФ В общем случае дискретный фильтр суммирует (с весовыми коэффициентами) некоторое количество входных отсчетов (включая последний) и некоторое количество предыдущих выходных отсчетов: (6.1) где a j и b i - вещественные коэффициенты . Данная формула называется алгоритмом дискретной фильтрации. Если по-иному сгруппировать слагаемые, чтобы с одной стороны от знака равенства были только входные отсчеты, а с другой — только выходные, получим форму записи, называемую разностным уравнением: (6.2)

2. Импульсная характеристика Выходная реакция на единичный импульс x a (k) называется импульсной характеристикой дискретной системы и обозначается h(k) . Как и в случае линейных систем с постоянными параметрами, знание импульсной характеристики позволяет проанализировать прохождение через дискретную систему любого сигнала. Действительно, прежде всего заметим, что произвольный сигнал x(k) можно представить в виде линейной комбинации единичных отсчетов: Выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик: (6.3)

Выражение (6. 3) называется дискретной сверткой (точнее, дискретной линейной сверткой — ее не следует путать с круговой сверткой, которая рассматривается при обсуждении свойств дискретного преобразования Фурье. Для физически реализуемой системы h(k) 0 при k , поэтому верхний предел суммирования в формуле (6. 3)) можно заменить на k . Это означает, что система при вычислении очередного отсчета может оперировать только прошлыми значениями входного сигнала и еще ничего не знает о будущих. Пример вычисления дискретной свертки, подробно иллюстрирующий выполняемые при этом математические операции, приведен на рис. 5.

Рис. 5 - Вычисление дискретной свертки

Как для любой дискретной системы для дискретного фильтра справедливо выражение дискретной свертки где y n – отсчеты выходного сигнала, x n-k – отсчеты выходного сигнала, задержанные на k периодов дискретизации, h k – отсчеты импульсной характеристики. Импульсной характеристикой дискретной системы называется реакция системы на сигнал типа δ-импульс при нулевых начальных условиях. Отсчеты импульсной последовательности можно получить, подавая на вход дискретной системы δ-импульс (рис. 5).

3. Устойчивость дискретных систем При отсутствии входного сигнала в дискретной системе могут существовать свободные колебания. Их вид зависит от начальных условий, то есть значений, хранящихся в эле-ментах памяти системы в момент отключения входного сигнала. Система называется устойчивой, если при любых начальных условиях свободные колебания являются затухающими, то есть если при x(k) - 0 Любой сигнал на выходе линейной стационарной системы представляет собой линейную комбинацию ее задержанных во времени импульсных характеристик. Поэтому для затухания свободных колебаний необходимо, чтобы была затухающей импульсная характеристика системы h(k) :

Дискретный фильтр называется устойчивым, если при произвольных начальных условиях реакция y n на любое ограниченное воздействие x n также ограничена, т.е. если , то , где . Критерием устойчивости дискретного фильтра является абсолютная сходимость ряда отсчетов импульсной характеристики: (6.4) Действительно, если представить в виде свертки входного сигнала и импульсной характеристики то откуда следует (6.4).

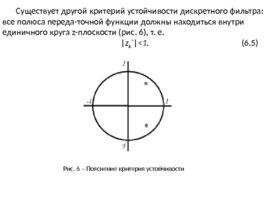
Существует другой критерий устойчивости дискретного фильтра: все полюса переда-точной функции должны находиться внутри единичного круга z-плоскости (рис. 6), т. е. z k (6.5) Рис. 6 – Пояснение критерия устойчивости

Действительно, так как то можно получить (6.6) Допустим, что , т.е. . Тогда и из выражения (6.6) получим: Для устойчивого фильтра должно выполняться условие (6. 4), т. е .

Следовательно, Н(z) должна быть конечна во всех точках z-плоскости, где z 1 . Очевидно, что в полюсе (при z z k ) H(z) . Отсюда следует, что передаточная функция не должна иметь полюсов на единичной окружности и вне ее, т. е. должно выполняться условие (6.5). Импульсная характеристика системы в общем случае содержит слагаемые вида где p i — полюсы функции передачи системы, n — неотрицательные целые числа, меньшие кратности полюса p i , А — некая константа. Такие слагаемые при k затухают, если полюс p i , по модулю меньше единицы: Таким образом, условие устойчивости: чтобы дискретная система была устойчива, полюсы ее функции передачи должны находиться па комплексной плоскости внутри круга единичного радиуса .