Презентация - Алгебра, 7 класс «системы линейных уравнений и способы их решения»

Алгебра, 7 класс «Системы линейных уравнений и способы их решения»

Знаете ли вы?
1. Какую математическую модель называют линейным уравнением с двумя переменными? 2. Что является решением системы уравнений с двумя переменными? 3. Что значит решить систему уравнений?

Способы решения систем уравнений
1. Графический способ. 2. Способ подстановки. 3. Способ сложения.

Алгоритм решения системы уравнений графическим способом

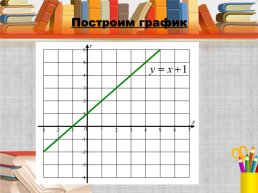
Решить систему уравнений
Рассмотрим первое уравнение
Выразим из этого уравнения y через x .
Для построения графика найдем две точки.

Построим график

Рассмотрим второе уравнение
Выразим из этого уравнения y через x .

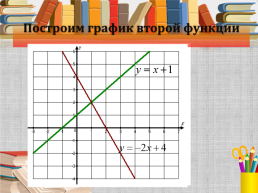
Построим график второй функции

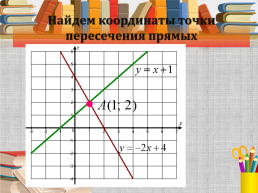
Найдем координаты точки пересечения прямых

Координаты точки пересечения прямых ― это решение системы
В этом случае говорят, что система решена графически

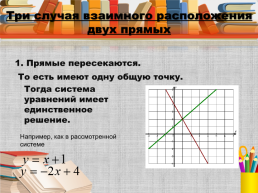
Три случая взаимного расположения двух прямых
1. Прямые пересекаются.
То есть имеют одну общую точку.
Тогда система уравнений имеет единственное решение.
Например, как в рассмотренной системе

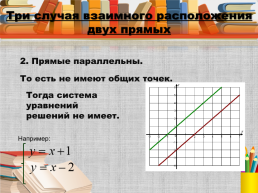
Три случая взаимного расположения двух прямых
2. Прямые параллельны.
То есть не имеют общих точек.
Тогда система уравнений решений не имеет.
Например:

Три случая взаимного расположения двух прямых
3. Прямые совпадают.
Например:
Тогда система уравнений имеет бесконечно много решений.

Но
при графическом способе решения системы уравнений обычно получается приближенное решение

Алгоритм решения системы уравнений способом подстановки

Способ подстановки
Этот способ удобен тогда, когда хотя бы один из коэффициентов при x или y равен 1 или -1.
Дана система уравнений
Рассмотрим каждое уравнение в отдельности.
1) Выразим одно из неизвестных через другое неизвестное из любого уравнения.

Способ подстановки
Вернемся в систему:
2) Полученное для y выражение подставим вместо данной неизвестной во второе уравнение.
Получилось уравнение с одной неизвестной

Способ подстановки
3) Решаем уравнение с одной неизвестной:
Возвращаемся к системе:

Способ подстановки
Возвращаемся к системе:
4) Подставим найденное значение x в первое уравнение и найдем вторую неизвестную
Запишем ответ.
Ответ:

Алгоритм решения системы уравнений способом сложения

Способ сложения
Задача 1. Решить систему уравнений
В тех случаях, когда в обоих линейных уравнениях системы при каком-либо из неизвестных коэффициентами являются противоположные числа, удобно применять способ алгебраического сложения уравнений.

Способ сложения
Сложим эти равенства почленно. В результате получим тоже верное равенство
+

Способ сложения
Вернемся в систему, записав одно из исходных уравнений и полученное значение x.
Подставим найденное значение x во второе уравнение, найдем вторую неизвестную.
Тогда пара чисел (5; 4) и будет решением системы.
Ответ:

Способ сложения
Задача 2. Решить систему уравнений
1) Выберем неизвестную (например x).
уравняем коэффициенты умножением на соответствующие числа.
2) Вычтем одно уравнение из другого.
3) Решим полученное уравнение с одним неизвестным

Способ сложения
4) Вернемся в систему, записав одно из исходных уравнений и полученное значение y
5)  Подставим найденное значение y в первое уравнение, найдем вторую неизвестную.
Тогда пара чисел (-3; 1) и будет решением системы.
Ответ:

Решите следующие системы уравнений:

Урок закончен.
Спасибо за внимание.